திட்ட விலக்கம் காணுதல்

1. தொகுக்கப்படாத தரவுகளின் திட்ட விலக்கம் காணுதல் 

(i) நேரடி முறை

(ii) கூட்டு சராசரி முறை 

(iii) ஊகச் சராசரி முறை

(iv) படி விலக்க முறை

2. தொடர் நிகழ்வெண் பரவலின் திட்ட விலக்கத்தினைக் கணக்கிடுதல்

(i) சராசரி முறை

(ii) எளிய முறை

(iii) படி விலக்க முறை

தொகுக்கப்படாத தரவுகளின் திட்ட விலக்கம் காணுதல் 

(i) நேரடி முறை

குறிப்பு

கொடுக்கப்பட்ட தரவுகளுக்குத் திட்டவிலக்கம் மற்றும் சராசரி ஒரே அலகில் அமையும்

குறிப்பு 

·  திட்டவிலக்கம் காணும்போது, தரவுப் புள்ளிகள் ஏறுவரிசையில் இருக்க வேண்டிய அவசியம் இல்லை. 

·  தரவுப் புள்ளிகள் நேரடியாகக் கொடுக்கப்பட்டிருந்தால் திட்ட விலக்கம் காண σ =   என்ற சூத்திரத்தைப் பயன்படுத்தலாம்.

· தரவுப் புள்ளிகள் நேரடியாகக் கொடுக்கப்படவில்லை, ஆனால் சராசரியிலிருந்து பெறப்பட்ட விலக்கங்களின் வர்க்கங்கள் கொடுக்கப்பட்டிருந்தால், நாம் திட்ட விலக்கம் காண σ =   என்ற சூத்திரத்தைப் பயன்படுத்தலாம்

எடுத்துக்காட்டு 8.4 

ஒரு வாரத்தின் ஒவ்வொரு நாளிலும் விற்கப்பட்ட தொலைக்காட்சிப் பெட்டிகளின் எண்ணிக்கை பின்வருமாறு 13, 8, 4, 9, 7, 12, 10. இந்தத் தரவின் திட்ட விலக்கம் காண்க.

தீர்வு

சிந்தனைக் களம் 

திட்டவிலக்கம், விலக்க வர்க்கச் சராசரியை விடப் பெரிதாக இருக்க முடியுமா? 

முன்னேற்றச் சோதனை 

விலக்க வர்க்கச் சராசரி 0.49 எனில், திட்ட விலக்கமானது ___________

(ii) கூட்டு சராசரி முறை 

திட்ட விலக்கத்தை காண கீழ்க்காணும் மற்றொரு சூத்திரத்தையும் பயன்படுத்தலாம்.

திட்ட விலக்கம் (கூட்டு சராசரி முறை) σ = 

இங்கு, di = xi –  எனில்,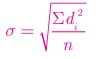

எடுத்துக்காட்டு 8.5 

ஒரு குறிப்பிட்ட பருவத்தில் 6 நாட்களில் பெய்யும் மழையின் அளவானது 17.8 செ.மீ, 19.2 செ.மீ, 16.3 செ.மீ, 12.5 செ.மீ, 12.8 செ.மீ, 11.4 செ.மீ எனில், இந்த தரவிற்கு திட்டவிலக்கம் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட தரவின் ஏறுவரிசையில் எழுதக்கிடைப்பது 11.4, 12.5, 12.8, 16.3, 17.8, 19.2 ஆகும். 

தரவுப் புள்ளிகளின் எண்ணிக்கை n = 6 

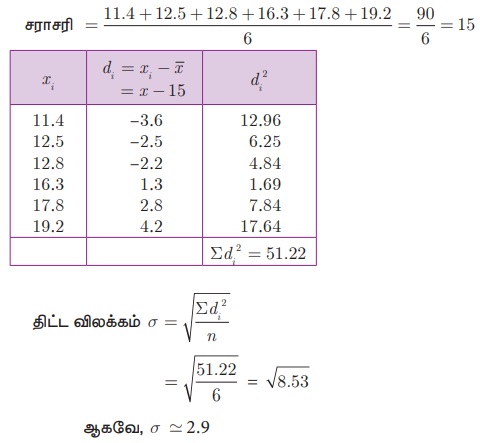
(iii) ஊகச் சராசரி முறை

சராசரியின் மதிப்பு முழுக்களாக இல்லாதபோது, ஊகச் சராசரி முறையைப் பயன்படுத்தி திட்ட விலக்கம் காண்பது சிறந்தது (ஏனெனில் தசமக் கணக்கீடுகள் சற்று கடினமாக இருக்கும் என்பதால்).

தரவுப் புள்ளிகளை x1, x2, x3, ..., xn என எடுத்துக் கொண்டால் -ஐ அதன் சராசரியாக கொள்ளலாம்.

xi -யிலிருந்து ஊகச் சராசரி (A) யின் விலகலே di ஆகும். (A ஆனது கொடுக்கப்பட்ட தரவுகளின் இடைப்பட்ட ஒரு தரவுப்புள்ளி).

di= xi − A ⇒ xi  = di + A ...(1)

Σdi= Σ(xi −A) 

= Σxi −(A + A + A + . . . to n முறைகள்)

Σdi = Σxi – A × n 

எடுத்துக்காட்டு 8.6 

ஒரு வகுப்புத் தேர்வில், 10 மாணவர்களின் மதிப்பெண்கள் 25, 29, 30, 33, 35,37, 38, 40, 44, 48 ஆகும். மாணவர்கள் பெற்ற மதிப்பெண்களின் திட்ட விலக்கத்தைக் காண்க. 

தீர்வு 

மதிப்பெண்களின் சராசரி = 35.9. இந்த மதிப்பானது தரவுகளின் நடுமதிப்பாக அமையும். அதனால் நாம் ஊகச் சராசரி A = 35, என எடுத்துக் கொள்கிறோம், மேலும், n = 10. 

(iv) படி விலக்க முறை

கொடுக்கப்பட்ட தரவுப் புள்ளிகளை x1, x2, x3,...xn   எனக் கருதுவோம். இதன் ஊகச் சராசரியை A எனக் கொள்ளலாம்.

xi - A -ன் பொது வகுத்தி c என்க.

குறிப்பு

மேலே கொடுக்கப்பட்டுள்ள முறைகளில் ஏதேனும் ஒரு முறையைப் பயன்படுத்தித் திட்ட விலக்கத்தைக் காணலாம்.

செயல்பாடு 1

காலாண்டுத் தேர்வு மற்றும் முதல் இடைத் தேர்வு ஆகியவற்றில் ஐந்து பாடங்களில் நீங்கள் பெற்ற மதிப்பெண்களைக் கொண்டு தனித்தனியாகத் திட்டவிலக்கம் காண்க. விடைகளிலிருந்து நீங்கள் என்ன தெரிந்து கொண்டீர்கள்?

எடுத்துக்காட்டு 8.7 

ஒரு பள்ளி சுற்றுலாவில் குழந்தைகள் தின்பண்டங்கள் வாங்குவதற்காக செலவு செய்த தொகையானது முறையே 5, 10, 15, 20, 25, 30, 35, 40 ஆகும். படி விலக்க முறையை பயன்படுத்தி அவர்கள் செய்த செலவிற்கு திட்ட விலக்கம் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட எல்லா தரவுப் புள்ளிகளும் 5 ஆல் வகுபடும் எண்கள். அதனால் நாம் ஊகச் சராசரி முறையைப் பின்பற்றலாம் A = 20, n = 8.

எடுத்துக்காட்டு 8.8 

கொடுக்கப்பட்டுள்ள தரவிற்கு திட்டவிலக்கம் காண்க. 7, 4, 8, 10, 11. இதன் எல்லா மதிப்புகளுடனும் 3-யை கூட்டும் போது கிடைக்கும் புதிய தரவிற்கு திட்டவிலக்கம் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட தரவுப் புள்ளிகளின் ஏறு வரிசை 4, 7, 8, 10, 11 மற்றும் n = 5

அனைத்து தரவுப் புள்ளிகளையும் 3 ஆல் கூட்டும் போது, நமக்கு கிடைக்கும் புதிய தரவுப் புள்ளிகள் 7,10,11,13,14 ஆகும்.

கொடுக்கப்பட்ட ஒவ்வொரு தரவுப் புள்ளியுடன் ஏதேனும் மாறிலி k-யைக் கூட்டினால், திட்ட விலக்கம் மாறாது.

எடுத்துக்காட்டு 8.9 

கொடுக்கப்பட்ட தரவின் திட்ட விலக்கம் காண்க 2,3,5,7,8. ஒவ்வொரு தரவுப் புள்ளியையும் 4 -ஆல் பெருக்கினால் கிடைக்கும் புதிய தரவின் மதிப்பிற்கு திட்ட விலக்கம் காண்க. 

தீர்வு 

கொடுக்கப்பட்டவை, n = 5

அனைத்து தரவுப் புள்ளிகளையும் 4ஆல் பெருக்கக் கிடைக்கும் புதிய தரவுப் புள்ளிகள் 8,12,20,28,32 ஆகும்.

கொடுக்கப்பட்ட ஒவ்வொரு தரவுப் புள்ளியையும் மாறிலி k-ஆல் பெருக்கும்போது கிடைக்கும் புதிய தரவின் திட்ட விலக்கம் k மடங்காக அதிகரிக்கிறது. 

எடுத்துக்காட்டு 8.10 

முதல் n இயல் எண்களின் சராசரி மற்றும் விலக்க வர்க்கச் சராசரிகளைக் காண்க.

தீர்வு 

தொகுக்கப்பட்ட தரவின் திட்ட விலக்கம் கணக்கிடல்

(i) சராசரி முறை

எடுத்துக்காட்டு 8.11 

ஒரு குறிப்பிட்ட வாரத்தில் 48 மாணவர்கள் தொலைக்காட்சி பார்ப்பதற்காகச் செலவிட்ட நேரம் கேட்டறியப்பட்டது. அந்தத் தகவலின் அடிப்படையில், கீழ்க்காணும் தரவின் திட்டவிலக்கம் காண்க.

தீர்வு 

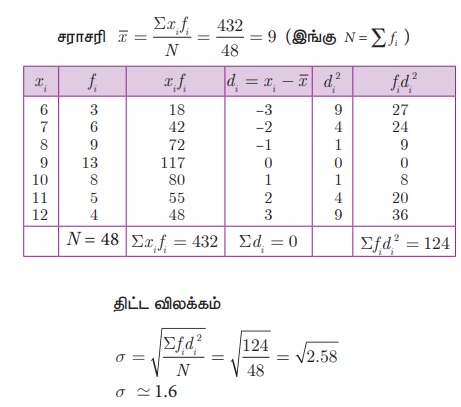
(ii) ஊகச் சராசரி முறை

x1, x2, x3 , ...xn  ஆகிய தரவுப் புள்ளிகளின் நிகழ்வெண்கள் முறையே f1 , f2, f3 , ... fn என்றும் என்பது சராசரி மற்றும் A என்பது ஊகச் சராசரி என்க.

எடுத்துக்காட்டு 8.12 

வகுப்புத் தேர்வில் மாணவர்கள் பெற்ற மதிப்பெண்கள் கீழே கொடுக்கப்பட்டுள்ளன. அவர்களின் மதிப்பெண்ணிற்குத் திட்ட விலக்கம் காண்க.

தீர்வு 

2. தொடர் நிகழ்வெண் பரவலின் திட்ட விலக்கத்தினைக் கணக்கிடுதல் 

(i) சராசரி முறை

திட்ட விலக்கம் , இங்கு xi என்பது i-ஆவது இடைவெளியின் மைய மதிப்பு fi என்பது i-ஆவது இடைவெளியின் நிகழ்வெண்.

(ii) எளிய முறை (அல்லது) படி விலக்க முறை

கணக்கீட்டைச் சுலபமாகச் செய்யக் கீழ்க்கண்ட சூத்திரம் கொடுக்கப்பட்டுள்ளது. இங்கு, A என்பது ஊகச் சராசரி, xi என்பது i -ஆம் இடைவெளியின் மைய மதிப்பு, மேலும் c என்பது இடைவெளியின் அகலம் ஆகும்.

எடுத்துக்காட்டு 8.13 

ஒரு வகுப்பிலுள்ள மாணவர்கள், குறிப்பிட்ட பாடத்தில் பெற்ற மதிப்பெண்கள் கீழ்க்கண்டவாறு கொடுக்கப்பட்டுள்ளன. 

இத்தரவிற்குத் திட்ட விலக்கம் காண்க.

தீர்வு 

ஊகச் சராசரி, A = 35, c = 10

சிந்தனைக் களம் 

(1) ஒரு தரவின் திட்டவிலக்கமானது 2.8 அனைத்துத் தரவுப் புள்ளிகளுடன் 5-ஐக் கூட்டினால் கிடைக்கும் புதிய திட்ட விலக்கமானது ____________.

(2) p, q, r ஆகியவற்றின் திட்ட விலக்கமானது S எனில், p- 3, q-3, r-3-யின் திட்ட விலக்கமானது _____________ ஆகும்.

எடுத்துக்காட்டு 8.14 

15 தரவுப் புள்ளிகளின் சராசரி மற்றும் திட்ட விலக்கம் முறையே 10, 5 என கண்டறியப்பட்டுள்ளது. அதை சரிபார்க்கும் பொழுது, கொடுக்கப்பட்டுள்ள ஒரு தரவுப் புள்ளி 8 என தவறுதலாக குறிக்கப்பட்டுள்ளது. அதன் சரியான தரவுப்புள்ளி 23 என இருந்தால் சரியான தரவின் சராசரி மற்றும் திட்ட விலக்கம் காண்க.

தீர்வு

தவறான மதிப்பு = 8, சரியான மதிப்பு = 23.

திருத்தப்பட்ட கூடுதல் = 150 – 8 + 23 = 165