Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ | Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї - Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї | 11th Mathematics : UNIT 1 : Sets, Relations and Functions
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 1 : Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї
Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї (Cartesian product)
Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я»Є Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«юЯ»ІЯ«ЪЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ Я«ЋЯ«БЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я«ЙЯ«»Я«┐Я«ЕЯ»Ї, A, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«єЯ«ЋЯ«┐Я«» Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«єЯ«ЋЯ«┐Я«» Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї (cartesian product), A ├Ќ B Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, A ├Ќ B = {(a, b):a Рѕѕ A, b Рѕѕ B} Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ, A, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«єЯ«ЋЯ«┐Я«» Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї,
A ├Ќ B ├Ќ C = {(a, b, c):a Рѕѕ A, b Рѕѕ B, c Рѕѕ C} Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«│Я«┐Я«цЯ«ЙЯ«Ћ, A ├Ќ A = {(a,b): a, b Рѕѕ A} Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.
A ├Ќ A = {(a, a): a Рѕѕ A} Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«Й?
Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«▒Я»ЇЯ«▒ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A = B Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я«ЕЯ»ЇЯ«▒Я«┐, A ├Ќ B РЅа B ├Ќ A Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»ЂЯ««Я«ЙЯ«ЕЯ«цЯ»ЂЯ««Я«ЙЯ«Е Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ A = B Я«јЯ«ЕЯ«┐Я«▓Я»Ї A ├Ќ B = B ├Ќ A.
РёЮ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,
РёЮ ├Ќ РёЮ = {(x,y):x, y Рѕѕ РёЮ} , РёЮ ├Ќ РёЮ ├Ќ РёЮ = {(x,y,z):x,y,z Рѕѕ РёЮ}.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ, РёЮ ├Ќ РёЮ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕ РёЮ2 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї РёЮ ├Ќ РёЮ ├Ќ РёЮ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕ РёЮ3 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. РёЮ ├Ќ РёЮ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«юЯ»ІЯ«ЪЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, РёЮ ├Ќ РёЮ ├Ќ РёЮ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ Я«ЋЯ«БЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, A = {1,2,3} Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B = {2,4,6} Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї
A ├Ќ B = {(1,2), (1,4), (1,6), (2, 2), (2,4), (2,6), (3, 2), (3,4), (3,6)}. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ A ├Ќ B Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ РёЮ ├Ќ РёЮ -Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«хЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«хЯ»ЂЯ««Я»Ї.
A ├Ќ B-Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, n (A ├Ќ B) = n(A) n(B) Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, n(A ├Ќ B ├Ќ C) = n(A) n(B) n(C). Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ A, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї РёЮ ├Ќ РёЮ -Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«Ћ Я«цЯ»єЯ«░Я«┐Я«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(i) {(x, 2 x): x Рѕѕ РёЮ}
(ii) {( x, x2): x Рѕѕ РёЮ}
(iii) {( x, Рѕџ x): x Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї}
(iv) {( x2, x): x Рѕѕ РёЮ}.
(v) {( x, - Рѕџ x): x Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї}
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.1 Я«ЋЯ«БЯ««Я»Ї A Я«єЯ«ЕЯ«цЯ»Ђ A = { x : x = 4n + 1, 2 РЅц n РЅц 5, n Рѕѕ РёЋ} Я«јЯ«ЕЯ«┐Я«▓Я»Ї, A-Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
A = { x : x = 4n + 1, n = 2,3,4,5} = {9,13,17,21}
Я«јЯ«ЕЯ«хЯ»Є n(A) = 4. n(P(A)) = 24 = 16
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.2 Я««Я«ЋЯ»ЇЯ«ЋЯ«│Я»ЇЯ«цЯ»іЯ«ЋЯ»ѕ 5000 Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«еЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«еЯ«ЪЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я««Я»іЯ«┤Я«┐ A Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 45%, Я««Я»іЯ«┤Я«┐ B Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 25%, Я««Я»іЯ«┤Я«┐ C Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 10% , A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я««Я»іЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 5%, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я««Я»іЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 4%, A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я««Я»іЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 4% Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я»іЯ«┤Я«┐Я«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 3% Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»іЯ«┤Я«┐ A Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«цЯ»ЇЯ«цЯ«ЕЯ»ѕ Я«фЯ»ЄЯ«░Я»Ї?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
Я«џЯ»єЯ«хЯ»ЇЯ«хЯ»єЯ«БЯ»ЇЯ««Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»єЯ«ЕЯ»ЇЯ«фЯ«ЪЯ««Я»Ї Я«јЯ«Е Я«ЄЯ«░Я»Ђ Я«хЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
(i) Я«џЯ»єЯ«хЯ»ЇЯ«хЯ»єЯ«БЯ»ЇЯ««Я»ѕ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я»Ї
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ n(A) = 5000 -Я«▓Я»Ї 45% = 2250 .
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ,
n(B) = 1250, n(C) = 500, n(A РѕЕ B) = 250, n(B РѕЕ C) = 200, n(C РѕЕ A) = 200
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n(A РѕЕ B РѕЕ C) = 150.
Я««Я»іЯ«┤Я«┐ A Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
n(A РѕЕ B' РѕЕ C') = n {A РѕЕ (B Рѕф C)'} = n(A) - n{A РѕЕ (B Рѕф C)}
= n(A) - n(A РѕЕ B) - n(A РѕЕ C) + n(A РѕЕ B РѕЕ C).
= 2250 - 250 - 200 + 150 = 1950.
A Я««Я»іЯ«┤Я«┐ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 1950.
(ii) Я«хЯ»єЯ«ЕЯ»ЇЯ«фЯ«ЪЯ««Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я»Ї:

Я«фЯ«ЪЯ««Я»Ї 1.1 РђЊЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, Я««Я»іЯ«┤Я«┐ A Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 39 Я«џЯ«цЯ«хЯ»ђЯ«цЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є Я««Я»іЯ«┤Я«┐ A Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї 5000 ├Ќ 39 / 100 = 1950.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.3 ((A Рѕф B' Рѕф C) РѕЕ (A РѕЕ B' РѕЕ C')) Рѕф ((A Рѕф B Рѕф C') РѕЕ (B' РѕЕ C')) = B' РѕЕ C'' Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
A РѕЕ B' РѕЕ C' Ріє A Ріє A Рѕф B' Рѕф C Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ»Ђ.
Я«јЯ«ЕЯ«хЯ»Є (A Рѕф B' Рѕф C) РѕЕ (A РѕЕ B' РѕЕ C') = A РѕЕ B' РѕЕ C'.
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї BРђЎ РѕЕ C' Ріє C' Ріє A Рѕф B Рѕф C'.
Я«јЯ«ЕЯ«хЯ»Є (A Рѕф B Рѕф C') РѕЕ (B' РѕЕ C') = B' РѕЕ C' Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, A РѕЕ B' РѕЕ C' Ріє B' РѕЕ C'.
Я«јЯ«ЕЯ«хЯ»Є ((A Рѕф B' Рѕф C) РѕЕ (A РѕЕ B' РѕЕ C')) Рѕф ((A Рѕф B Рѕф C') РѕЕ (B' РѕЕ C')) = B' РѕЕ C'
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: Я«хЯ»єЯ«ЕЯ»ЇЯ«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«»Я«▒Я»ЇЯ«џЯ«┐ Я«џЯ»єЯ«»Я»ЇЯ«»Я«хЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.4 X = {1,2,3, ..., 10} Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A = {1,2,3,4,5} Я«јЯ«ЕЯ«┐Я«▓Я»Ї, A - B = {4} Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» X -Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ B Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ B Ріє X Я«јЯ«цЯ»ЇЯ«цЯ«ЕЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
{6,7,8,9,10} Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ««Я«ЙЯ«ЋЯ«┐Я«» C Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ, B = C U {1,2,3,5} Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ A - B = {4} Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒ Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї X Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ B Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ЂЯ««Я»Ї, {6,7,8,9,10} Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«џЯ««Я««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, B Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 25 = 32.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.5 A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, n (B- A) = 2 n (A РђЊ B) = 4 n(A РѕЕ B) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n(A U B) = 14 Я«јЯ«Е Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, n(P(A)) Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
n(P(A)) -Я«љЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б n(A) Я«цЯ»ЄЯ«хЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
n(A РѕЕ B) = k Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»Є, n(A РђЊ B) = 2k Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (B РђЊ A) = 4k Я«єЯ«ЋЯ»ЂЯ««Я»Ї .
Я«ЄЯ«еЯ»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї, n (A Рѕф B) = n (A - B) + n (B - A) + n (A РѕЕ B) = 7k
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, n (A Рѕф B) = 14 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї 7k = 14, k = 2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, n (A РђЊ B) = 4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (B - A) = 8
n (A) = n (A - B) + n (A РѕЕ B) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї n(A) = 6.
Я«јЯ«ЕЯ«хЯ»Є, n(P(A)) = 26 = 64 .
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.6 Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї k Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕ Я«хЯ«┐Я«Ъ 112 Я«ЁЯ«цЯ«┐Я«ЋЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї, m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї k Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
n (A) = m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (B) = k Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«јЯ«ЕЯ»ЇЯ«Ћ. B Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«Ъ A Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї, m > k. Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ 2m РђЊ 2k = 112.
Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, 2k( ) 2m-k РђЊ 1) = 24 ├Ќ 7
Я«ЄЯ«еЯ»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Є Я«џЯ«ЙЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»Ђ k = 4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 2m-k - 1 = 7 Я«єЯ«ЋЯ»ЂЯ««Я»Ї . Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї m - k = 3 . Я«јЯ«ЕЯ«хЯ»Є m = 7.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.7 n (A) = 10 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (A РѕЕ B) = 3 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n (( A РѕЕ B)Рђ▓ РѕЕ A ) -Я«љ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:

Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.8
A = { 1,2,3,4} Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B = { 3,4,5,6} Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n (A U B) ├Ќ (A РѕЕ B) ├Ќ (A ╬ћ B) -Я«љ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
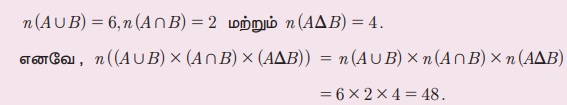
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 1.9
P(A) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ A Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, n(P(P(P ¤є)))) -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
P(¤є) Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї P(P(¤є) Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 21 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї, P(P(P(¤є))) Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 22 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ 4 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 1.1
1. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
(i) { x Рѕѕ РёЋ : x2 < 121 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ«Й Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї}.
(ii) (x-1) (x+1) (x2-1) = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я«┐Я«ЋЯ»ѕ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я»Ї.
(iii) {x Рѕѕ РёЋ: 4x + 9 < 52}.
(iv) { x: x-4/x+2 = 3, x Рѕѕ РёЮ - {-2}}.
2. {-1. 1} Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ
3. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«хЯ«ЕЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»Ї Я«јЯ«хЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«БЯ««Я»Ї, Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»ЇЯ«▓Я«ЙЯ«ц Я«ЋЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«Ћ.
(i) {x Рѕѕ РёЋ: x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«фЯ«ЋЯ«Й Я«јЯ«БЯ»Ї}.
(ii) {x Рѕѕ РёЋ: x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«фЯ«ЋЯ«Й Я«јЯ«БЯ»Ї}.
(iii) {x Рѕѕ Рёц: x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«ЪЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї).
(iv) {x Рѕѕ РёЮ: x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї}.
(v) {x Рѕѕ РёЋ: x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї}.
4. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ, Я«цЯ«ЋЯ»ЂЯ«еЯ»ЇЯ«ц A, B, C Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
(i) A ├Ќ (B РѕЕ C) = (A ├Ќ B) РѕЕ (A ├Ќ C).
(ii) A ├Ќ (B Рѕф C) = (A ├Ќ B) Рѕф (A ├Ќ C).
(iii) (A ├Ќ B) РѕЕ (B ├Ќ A) = (A РѕЕ B) ├Ќ (B РѕЕ A).
(iv) C - (B - A) = (C РѕЕ A) Рѕф (C РѕЕ B').
(v) (B - A) РѕЕ C = (B РѕЕ C) РђЊ A = B РѕЕ (C - A).
(vi) (B - A) Рѕф C = (B Рѕф C) РђЊ (A - C).
5. "Я«њЯ«░Я»Ђ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЊЯ«░Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Є Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ«БЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я«ЙЯ«цЯ»Ђ" Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«цЯ»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ѕ Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«Ћ.
6. n(P(A)) = 1024, n (A Рѕф B) = 15 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї m (P(B)) = 32 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n (A РѕЕ B) Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ
7. n (A РѕЕ B) = 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (A Рѕф B) = 10 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n(P(AРѕєB)) Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
8. A ├Ќ A Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 16 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї (1, 3) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (0, 2) Я«јЯ«ЕЯ«┐Я«▓Я»Ї, A -Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
9. n(A) = 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n (B) = 2 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЪЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A, B Я«єЯ«ЋЯ»ЂЯ««Я»Ї. (x, 1), (y, 2), (z, 1) Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ A ├Ќ B Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«џЯ«┐Я«▓ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, A, B Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ x, y, z Я««Я»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї)
10. A ├Ќ A Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 16 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. S = {(a,b) Рѕѕ A├ЌA:a < b} Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї (-1, 2) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (0, 1) Я«јЯ«ЕЯ«┐Я«▓Я»Ї S Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ђЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.