சமபரப்பு அல்லது லாம்பர்ட் உருளைக் கோட்டுச்சட்டம்

சில தேர்வு செய்யப்பட்ட நிலவரைபடக் கோட்டுச் சட்டங்களை உருவாக்கும் முறைகள் (Construction of some selected Projections)

1. சமபரப்பு அல்லது லாம்பர்ட் உருளைக் கோட்டுச்சட்டம் (Cylindrical Equal Area Projection / Lambert's Equal Area Projection)

இதை 1772ஆம் ஆண்டு J.H.லாம்பர்ட் என்பவர் வடிவமைத்தார். இது இயல்பான இயலுரு தோற்றக் கோட்டுச் சட்டத்தில் உள்ளது. இவற்றின் தொடு கோடானது புவியிடைக் கோட்டில் இருக்கும்.

சமபரப்பு உருளைக் கோட்டுச்சட்டத்தின் பண்புகள்

1. அட்ச, தீர்க்க ரேகைகள் நேர்கோடுகள் ஆகும்.

2. அட்ச, தீர்க்க ரேகைகள் ஒன்றையொன்று செங்கோணத்தில் வெட்டிக் கொள்கின்றன.

3. இக்கோட்டுச்சட்டத்தில் அட்சரேகைகளுக்கு இடைப்பட்ட தூரம் புவியிடைக் கோட்டிலிருந்து துருவத்தை நோக்கிச் செல்லச் செல்ல குறைகிறது. ஆனால் தீர்க்க ரேகைகளுக்கு இடைப்பட்ட தூரம் சமமாக காணப்படுகிறது.

4. அட்ச ரேகைகள் புவியிடைக் கோட்டிற்கு இணையாக அதன் அளவிற்கே வரையப்பட்டுள்ளது. எனவே, புவியிடைக் கோட்டை ஒட்டிய அளவை சரியானதாக இருக்கும்.

எடுத்துக்காட்டு 10.1

2 செ.மீ. ஆரமுள்ள சுருக்கப்பட்ட கோளத்தைக் கொண்டு ஒரு சம்பரப்பு உருளைக் கோட்டுச் சட்டம் வரைக. அதன் அட்ச மற்றும் தீர்க்க ரேகைகளின் இடைவெளி 30° ஆகும்.

வரையும் முறை

• 2 செ.மீ ஆரத்தில் ) வை மையமாகக் கொண்டு ஒரு வட்டம் வரைய வேண்டும்.

• W£என்ற புவியிடை அச்சினையும்  NS என்ற துருவ அச்சினையும் வரைய வேண்டும்.

• 30° மற்றும் 60° கோணத்தை (இரண்டு) வட மற்றும் தென் அரை கோளத்தில் குறிக்க வேண்டும். கோணங்களை முறையே B, C, B மற்றும் C' என்று குறிக்கவும்.

• W£என்ற கோட்டினை E' வரை நீட்டிவிட வேண்டும்.

• £B என்ற அளவில் ££ கோட்டினை 12 (360/30) சம பாகங்களாக பிரிக்க வேண்டும். இந்தக் கோடு புவியிடைக் கோட்டினை குறிக்கும்.

• பிரிக்கப்பட்ட புள்ளிகள் வழியாக செங்குத்து கோடுகள் வரைக. இவை தீர்க்கக் கோடுகளை குறிக்கும்.

• ££ என்ற கோட்டிற்கு இணைகோடுகள் N, C, B, B', C' மற்றும் S லிருந்து வரைக. இவை 30°, 60° மற்றும் 90° அட்சரேகைகளை குறிக்கின்றது. படத்தில் உள்ளவாறு கோட்டுச் சட்டத்தினை பூர்த்தி செய்ய வேண்டும்.

2. சம தூர உருளைக் கோட்டுச்சட்டம் (Cylindrical Equi - Distant Projection)

பொ.ஆ 100ல் மாரினஸ் (Marinus of Tyre) என்பவர் சமதூர உருளைக் கோட்டு சட்டத்தினை வடிவமைத்தார். இந்த கோட்டுச் சட்டத்தில் தொடு கோடானது புவியிடைக் கோட்டினை ஒட்டி இருக்கும்.

சமதூர உருளை கோட்டுச் சட்டத்தின் பண்புகள்

• துருவங்கள் நேர் கோடுகளாகவும் புவியிடைக் கோட்டிற்கு சமமாகவும் இருக்கும்.

• தீர்க்கரேகைகள் இணைக்கோடுகளாகவும் சமதூர இடைவெளி கொண்டு மற்றும் புவியிடைக் கோட்டின் பாதி அளவில் இருக்கின்றன.

• அட்ச ரேகைகள் நேர் கோடுகளாக, சமதூர இடைவெளி கொண்டு, தீர்க்கரேகைகளுக்கு செங்குத்தாகவும் மற்றும் அவை புவியிடைக் கோட்டின் நீளத்திற்கு சமமாகவும் இருக்கும்.

• நிலவரைபட புவியிடைக் கோட்டின் நீளமானது கோளத்தில் உள்ள அளவிற்கு சமமாக இருக்கும். ஆனால் அளவை புவியிடைக் கோட்டில் உண்மையாக காணப்படும் அட்ச ரேகைகளில் இருக்காது.

• அட்ச மற்றும் தீர்க்க ரேகைகளுக்கிடையே உள்ள தூரம் நிலவரைபடம் முழுவதும் சமமாக இருக்கும்.

• இக்கோட்டுச் சட்டம் சம்பரப்பு கோட்டுச் சட்டமாகவும், உருவமொத்த உருளை கோட்டுச் சட்டமாகவும் இல்லாததால் இதுபொது நோக்கங்களுக்கு மட்டும் பயன்படுகிறது.

எடுத்துக்காட்டு 10.2

2 செ.மீ. ஆரமுள்ள சுருக்கப்பட்ட கோளத்தைக் கொண்டு ஒரு சமதூர உருளைக் கோட்டுச் சட்டம் வரைக. அதன் அட்ச மற்றும் தீர்க்க ரேகைகளின் இடைவெளி 30.

வரையும் முறை

• 2 செ.மீ. ஆரத்தில் வை மையமாகக் கொண்டு ஒரு வட்டம் வரைய வேண்டும்.

• 30° கோணத்தை வட அரைகோளத்தில் காட்டி C என்று குறிக்க வேண்டும். • AB என்ற ஒரு நீண்ட கோடு வரைய வேண்டும். அது புவியிடைக் கோட்டை குறிக்கும்.

• தீர்க்க ரேகையினை 30° இடைவெளியில் வரைவதால் AB கோட்டினை 12 (360/30) சமபாகங்களாக EC என்ற அளவைக் கொண்டு பிரிக்க வேண்டும்.

• தீர்க்க ரேகைகளை வரைய , AB கோட்டின் பிரிக்கப்பட்ட புள்ளிகளின் வழியாக, செங்குத்து கோடுகள் வரைய வேண்டும்.

• தீர்க்க ரேகைகளின் 180°ல் மற்றும் அட்சரேகையினை 30° இடைவெளியில் வரைவதால் (180/30) பாகங்களாக பிரிக்க வேண்டும். அதாவது 6 பாகங்களாக பிரிக்க வேண்டும்.

• இப்புள்ளிகளின் வழியாக, புவியிடைக் கோட்டிற்கு இணையாக கோடுகள் வரைய வேண்டும். படத்தில் உள்ளவாறு கோட்டுச்சட்டத்தினை பூர்த்தி செய்ய வேண்டும்.

3. துருவ உச்சிக் கோட்டுச் சட்டங்கள் (Polar Zenithal Projection)

இக்கோட்டுச் சட்டத்தினை J.H. லாம்பெர்ட் என்பவர் வடிவமைத்தார். இதனை லாம்பெர்ட்டின் சம்பரப்பு உச்சிக்கோட்டுச் சட்டம் என்றும் அழைப்பார்கள்.

• துருவம் உச்சி கோட்டுச் சட்டத்தில் மையமாகவும் மற்றும் அட்ச ரேகைகள் ஒரு மைய வட்ட வளையங்களாகவும் காணப்படுகின்றன.

• தீர்க்க ரேகைகள் அவற்றிக்கு இடையேயான சரியான கோண இடைவெளியைக் கொண்டு நேர்கோடுகளாக துருவத்திலிருந்து வருகின்றன.

• அட்ச, தீர்க்க ரேகைகள் ஒன்றையொன்று செங்கோணத்தில் வெட்டிக் கொள்கின்றன.

• அட்சரேகைகள் வழியே அளவையானது கோட்டுச் சட்டத்தின் மையத்திலிருந்து அதிகரிக்கிறது.

• இந்த அதிகரிப்பு தீர்க்க ரேகைகள் இடைவெளி விகிதக் குறைவினால் சமப்படுத்தப்படுவதினால் பரப்பில் மாற்றமின்றிக் காட்டப்படுகின்றது. எனவே, இது ஒரு சம்பரப்புக் கோட்டுச் சட்டமாகும்.

• மையத்திலிருந்து அட்சரேகைகளுக்கு இடைப்பட்ட தூரம் விளிம்பினை நோக்கிக் குறைந்து கொண்டே செல்கிறது.

• துருவ பகுதிகளின் அரசியல் பிரிவு மற்றும் பரவல்களை குறிக்க இந்த கோட்டுச் சட்டம் பயன்படுகின்றது. இவை வட அரை கோளத்தின் பெரிய பரப்புகளை குறிக்கவும் பயன்படுகிறது.

எடுத்துக்காட்டு 10.3

4 செ.மீ. ஆரமுள்ள சுருக்கப்பட்ட கோளத்தை கொண்டு ஒரு துருவ சம்பரப்பு உச்சி கோட்டுச் சட்டம் வரைக. அதன் அட்ச மற்றும் தீர்க்க ரேகைகளின் இடைவெளி 30° ஆகும்.

வரையும் முறை

• 4செ.மீ. ஆரத்தில் 0வை மையமாகக் கொண்டு ஒரு வட்டம் வரைய வேண்டும். இதில் CD என்ற துருவ அச்சினையும் AB என்ற புவியிடைக் கோட்டினையும் வரைய வேண்டும். இவை வில் ஒன்றையொன்று செங்கோணத்தில் வெட்டிக் கொள்கின்றன

• 30°, 60 மற்றும் 90° என்ற கோண அளவுகளை குறித்து OE, OF, OC என்று குறிக்க வேண்டும். பிறகு, CB, CE மற்றும் CFவை நேர்கோடுகளாக இணைக்க வேண்டும்.

• CF என்ற இடைப்பட்ட தூரத்தை மையமாக கொண்டு ஒரு வட்டம் வரைய வேண்டும். அப்புள்ளியை N என்று குறிக்கவும். இவை 60 அட்சரேகையை குறிக்கும். அதேபோல் Nயை மையமாக வைத்து CE மற்றும் CB என்ற இடைப்பட்ட தூரத்தை கொண்டு 60°, 30° மற்றும் 0° அட்சரேகைக்கு ஒரு மைய வட்ட வளையங்கள் வரைய வேண்டும்.

• N யை மையப்புள்ளியாகக் கொண்டு, பாகைமானியைப் பயன்படுத்தி 30° கோண அளவை கொண்டு மற்ற தீர்க்க ரேகைகளை குறிக்க வேண்டும்.

• படத்தில் உள்ளவாறு கோட்டுச் சட்டத்தினை பூர்த்தி செய்ய வேண்டும்.

            துருவ சமபரப்பு உச்சி கோட்டுச் சட்டம்

துருவ சமபரப்பு உச்சி கோட்டுச் சட்டம்

துருவ சமதூர உச்சிக் கோட்டுச் சட்டத்தின் பண்புகள்

• துருவம் இக்கோட்டுச் சட்டத்தின் மையமாகவும் மற்றும் அட்சரேகைகள் ஒருமைய வட்ட வளையங்களாகவும் இருக்கும்

• தீர்க்க ரேகைகள் அவற்றிக்கிடையில் சரியான கோண இடைவெளியைக் கொண்டு நேர்கோடுகளாக துருவத்திலிருந்து வெளிவருகின்றன.

• அட்ச, தீர்க்க ரேகைகள் நேர்கோணத்தில் ஒன்றையொன்று வெட்டிக் கொள்கின்றன.

• அட்சரேகைகள் ஒன்றிலிருந்து மற்றொன்றிக்கு உண்மையான தூரத்தில் வரையப்பட்டுள்ளன.

• இக்கோட்டுச் சட்டத்தின் மையத்திலிருந்து அட்சரேகைகளின் அளவை அதிகரிக்கின்றன.

• இது துருவ பகுதிகளைக் காட்ட பயன்படுத்தப்படுகிறது.

எடுத்துக்காட்டு 10.4

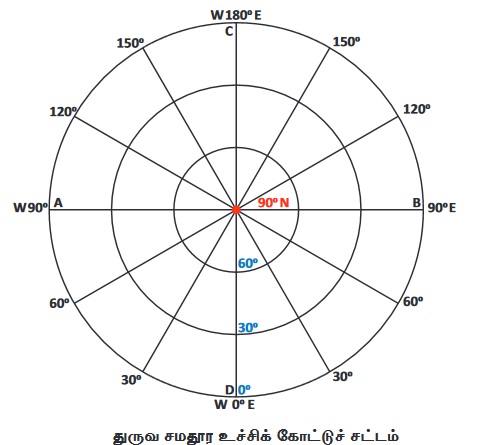
3 செ.மீ. ஆரமுள்ள சுருக்கப்பட்ட கோளத்தை கொண்டு ஒரு துருவ சமதூர உச்சிக் கோட்டு சட்டம் வரைக. அதன் அட்ச மற்றும் தீர்க்க இடைவெளி 30° ஆகும்.

வரையும் முறை

• 3செ.மீ. ஆரத்தில் வை மையமாகக் கொண்டு ஒரு வட்டம் வரைய வேண்டும்.

• 30° கோணத்தை குறித்து AOB என்று குறிப்பிட வேண்டும்.

• பிறகு AB என்ற ஆரத்தில் N யை மையமாகக் கொண்டு ஒரு வட்டம் வரைய வேண்டும்.

• CD என்ற துருவ அச்சினையும் AB என்ற புவியிடைக் கோட்டினையும் வரைய வேண்டும். இவை 0 வில் ஒன்றையொன்று செங்கோணத்தில் வெட்டி கொள்கின்றன.

• இடைவெளியின் எண்ணிக்கை = 90/30 = 3

• N யை மையமாகக் கொண்டு மூன்று ஒரு மைய வட்ட வளையங்கள் வரைய வேண்டும்.

• பாகைமானியை பயன்படுத்தி 30° கோண அளவை கொண்டு மற்ற தீர்க்க ரேகைகளை குறிக்க வேண்டும்.

• படத்தில் உள்ளவாறு கோட்டுச் சட்டத்தினை பூர்த்தி செய்ய வேண்டும்.