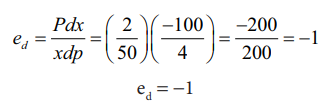வகை நுண்கணிதம் [Differential Calculus)

வகை நுண்கணிதம் [Differential Calculus)

1. பொருள்

நுண்கணிதத்தின் அடிப்படை செயலி வகையீடு (differentiation) ஆகும். எந்த ஒரு சார்பின் மாற்ற வீதத்தை விளக்கிட வகைக்கெழு பயன்படுகிறது. வகைக்கெழு என்பது சார்பற்ற மாறியில் ஏற்படும் சிறிய மாற்றத்திற்கு (பூஜ்ஜியத்திற்கு நெருக்கமாக) ஏற்ப சார்ந்த மாறியில் ஏற்படும் மாற்றமாகும்.

y = f(x) ஒரு சார்பு என்க.

x ஐப் பொறுத்து y ஐ வகைப்படுத்திட

d(y) / dx = df (x) / dx

2. வகையீட்டின் சில முக்கிய சூத்திரங்கள் (திட்ட வடிவங்கள்)

(மாறிலி, கூட்டல், கழித்தல் மட்டும்) 

1. d(c) / dx = 0 இங்கு C ஒரு மாறிலி

 ( 'x' ஐப் பொறுத்து 'C' ஐ வகையிட மதிப்பு சுழியம் என படிக்கவும்)

2. d(xn) / dx = nxn-1

3. d(x) / dx = 1x1-1 = 1x° = 1

4. d(u + v) / dx = du / dx + dv / dx

5. d(u-v) / dx = du / dx – dv / dx

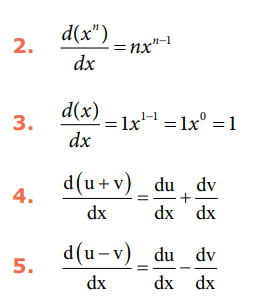
குறிப்பு:

எந்த ஒரு சுழியம் அல்லாத மெய் எண்ணிற்கும் அடுக்கு சுழியமெனில் மதிப்பு 

1. x ≠ 0 என்றால் x° = 1

எடுத்துக்காட்டு: 12.12 

Y = 4, எனில் dy dy / dx மதிப்பு காண்.

தீர்வு :

Y = 4, இங்கு 4 மாறிலி மதிப்பு. மாறிலிச்சார்பின் வகைக்கெழு சுழியம்.

எனவே, dy / dx = d(4) / dx = 0

எடுத்துக்காட்டு: 12.13

y = 6x3 என்ற சார்பின் சாய்வினைக் காண்க

தீர்வு:

y = 6x3 தரப்பட்டுள்ளது

சாய்வு = dy / dx

dy / dx  = 6 (3) x3-1 = 18x2 (x ன் எந்த ஒரு மதிப்பிற்கும்)

எடுத்துக்காட்டு: 12.14 

y=5x4 என்ற சார்புக்கு x = 10 எனும் போது சாய்வு என்ன?

தீர்வு :

y = 5x4 சமன்பாடு தரப்பட்டுள்ளது

சாய்வு = dy / dx

dy / dx = 5 (4) x4-1 

= 20x3 

x = 10 என இருக்கும் போது சாய்வு = 20 (10)3

= 20,000,

சாய்வு = 20,000

எடுத்துக்காட்டு: 12.15 

Y = 3x2 + 16x3 என்ற சார்பினை x ஐ பொருத்து வகையிடுக.

தீர்வு :

Y = 3x2 + 16x3 ஐ வகையிட

dy / dx = 3(2)x2-1 +16 (3)x3-1

= 6x1 + 48x2

dy / dx = 6x + 48x2

எடுத்துக்காட்டு: 12.16

Y = 2x3 – 6x, எனில் dy / dx ஐ காண்க.

தீர்வு :

Y = 2x3 – 6x

x ஐ பொருத்து 'y' யினை வகையிட,

dy / dx = 2(3)x3-1 - 6(1)x1-1

= 6x2 - 6x° 

dy / dx = 6x2 – 6

3. வகை நுண்கணிதத்தின் பயன்பாடு

இரண்டு அல்லது இரண்டுக்கு மேற்பட்ட மாறிகளின் உறவினை சார்பாக விளக்கலாம். தொடர்ச்சியான சார்பினை மட்டுமே வகைபடுத்த முடியும். உதாரணமாக, வகை நுண்கணிதமானது பின்வருவனவற்றை காண பயன்படுகிறது. 

1. விலையைப் பொறுத்து தேவையில் ஏற்படும் மாற்ற வீதம். (நுண்ணினப் பொருளியலில்) 

2. முதலீட்டினை பொறுத்து வருமானத்தில் ஏற்படும் மாற்ற வீதம் (பேரினப் பொருளியலில்)

4. இறுதிநிலை கருத்துகள்

X ல் ஏற்படும் சிறு மாறுபாட்டிற்கு ஏற்ப Y ல் ஏற்படும் மாறுபாடுகள் இறுதிநிலை கருத்து எனப்படுகிறது. (X என்பது சாராத மாறியாகும், Y என்பது சார்ந்த மாறியாகும்)

5. இறுதிநிலை உற்பத்தி 

உற்பத்தி காரணியின் இறுதிநிலை உற்பத்தி என்பது ஒரு கூடுதல் அலகு உற்பத்திக் காரணியை பயன்படுத்துவதால் மொத்த உற்பத்தியில் ஏற்படும் கூடுதல் அளவாகும்.

MP = d(TP) / dQ அல்லது ΔTP / ΔQ

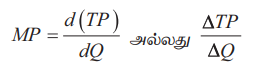
6. இறுதிநிலை செலவு

இறுதிநிலை செலவு என்பது ஓர் அலகு உற்பத்தி அதிகரிப்பினால் மொத்த செலவில் ஏற்படுகிற கூடுதல் செலவாகும். குறியீட்டில்,

MC = d (TC) / dQ அல்லது MC = ΔTC / ΔQ

இங்கு ΔTC என்பது மொத்தச் செலவில் ஏற்படும் மாற்றத்தை குறிக்கிறது; ΔQ என்பது அளவு அல்லது வெளியீட்டில் ஏற்படும் சிறு மாற்றத்தை குறிப்பிடுகிறது. (பொருளியலில் ஒரு வேலை செய்யும் நபர், ஒரு வெளியீடு என்பன மிகச்சிறிய அலகாக கருதப்படுகிறது) 

எடுத்துக்காட்டு: 12.17

TC = 15 + 3Q2 + 7Q3 என்பது மொத்த செலவுச் சார்பு என தரப்படின் இறுதிநிலைச் செலவுச் சார்பினை வருவி.

தீர்வு :

TC = 15 + 3Q2 +7Q3

MC = d(15) / dQ + d(3Q2) / dQ + d(7Q3)/dQ

= 0 + 3(2)Q2-1 + 7(3)Q3-1 

MC = 6Q +21Q2

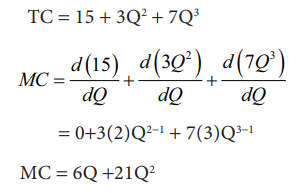
7. இறுதிநிலை வருவாய்

இறுதிநிலை வருவாய் என்பது கூடுதல் ஓர் அலகு உற்பத்தியினை விற்பதனால் ஈட்டப்பட்ட வருவாய் ஆகும். வேறு விதமாகக் கூறினால், இறுதிநிலை வருவாய் என்பது ஒரு அலகு கூடுதல் பொருளை விற்பதால் மொத்த வருவாயில் ஏற்படும் கூடுதலாகும்.

MR = d(TR) / dQ அல்லது = ΔTR / ΔQ

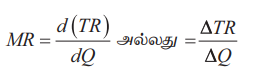
இங்கு ΔTR என்பது மொத்த வருவாயில் ஏற்படும் மாற்றத்தையும், ΔQ என்பது வெளியீட்டில் ஏற்படும் மாற்றத்தையும் குறிக்கும்.

எடுத்துக்காட்டு: 12.18

TR = 50Q – 4Q2 என தரப்பட்டுள்ளது. Q = 3 எனில் இறுதிநிலை வருவாயைக் காண்க.

தீர்வு :

TR = 50Q – 4Q2

MR = d(TR)/dQ

MR = 50(1)Q1-1 – 4(2)Q2-1

= 50(1)Q° - 8Q1

= 50(1) - 8Q (ஃQ° = 1, Q1 = Q) 

MR = 50 - 8Q

Q = 3 எனும்போது 

MR = 50 -8(3) =26

எடுத்துக்காட்டு: 12.19

ஓர் உற்பத்தியாளரின் மொத்த செலவுச் சார்பு TC (Q) = Q3 - 18Q2 + 91Q + 10 ஆகும். இங்கு செலவுகள் ரூபாயில் உள்ளன. Q = 3 என்கின்றபோது இறுதிநிலை செலவு (MC) மற்றும் சராசரி மாறும் செலவு (AVC) காண்க.

தீர்வு :

TC(Q) = Q3-18Q2 +91Q +10 தரப்பட்டுள்ளது. இறுதிநிலை செலவுச்சார்பினை காண Q ஐ பொருத்து வகைப்படுத்த,

MC (Q) = d(TC) / dQ = 3Q3-1 - 18(2)Q2-1 + 91(1)Q1-1 + 0

= 3Q2 – 36Q1 + 91Q0 + 0

MC (Q) = 3Q2 – 36Q + 91 (∴ Q0 = 1)

Q = 3 எனில்

MC(Q) = 3(32)-36(3)+91

= 3(9)-108+91

= 27-108+91

= 118-108

= 10 

சராசரி மாறும் செலவு காண (AVC) 

TC(Q) = Q3 - 18Q2 + 91Q + 10 தரப்பட்டுள்ளது. 

TVC (Q) = Q3 - 18Q2 + 91Q என அறிகிறோம். 

(மாறிலி மதிப்பு என்பது மாறாச் செலவு ஆகும்.)

AVC(Q) = TVC(Q)/Q

AVC(Q) = Q2 - 18Q + 91

Q = 3 எனில்,

AVC(Q) = 32 -18(3) + 91

= 9 -54 + 91

= 100 - 54 = 46

ஃ AVC(Q) = Q3 -18Q2 + 91Q / Q

= Q2 - 18Q + 91 

குறிப்பு : மாறாச் செலவு = 10

சராசரி மாறாச்செலவு = 10 / Q

சராசரி செலவு = Q3 -18Q2 + 91Q + 10 / Q

= Q2 -18Q + 91 + 10 / Q

எனவே சராசரி செலவு = AVC + AFC

AC = AVC + AFC

AC = TC / Q

எடுத்துக்காட்டு: 12.20 

ஒரு குறிப்பிட்ட பண்டத்தை உற்பத்தி செய்ய ஒவ்வொரு மாதத்தின் மொத்தச் செலவுகளை தயாரிப்பாளர் ஒருவர் TC(Q) = 128 + 60Q + 8Q2 என மதிப்பிடுகிறார். இறுதிநிலை செலவு, சராசரி செலவு, மாறாச் செலவு, மாறும் செலவு, சராசரி மாறாச் செலவு, சராசரி மாறும் செலவு ஆகியவற்றைக் காண்க.

தீர்வு :

TC(Q) = 128 + 60Q + 8Q2 கொடுக்கப்பட்டுள்ளது. 

TC = மாறாச் செலவு + மாறும் செலவு என்பதை அறிவோம்

MC (Q) = d(TC) / dQ

= 0 + 60(1)Q1-1 + 8(2) Q2-1 

= 0 + 60Q0 + 16Q1(Since, Q0 = 1)

MC = 60 + 16Q

சராசரி செலவு= TC / Q

= 128+60Q +8Q2 / Q

AC = 128/Q +60+8Q

மாறிலி மதிப்பினை மாறாச்செலவு என்கிறோம் 

மாறாச் செலவு = 128

FC = 128 

சராசரி மாறாச்செலவு = 128 / Q

AFC = 128 / Q

சராசரி மாறும் செலவு = 60 + 8Q (மாறும் செலவினை Q ஆல் வகுக்க)

∴AVC = 60 + 8Q

8. தேவை நெகிழ்ச்சி

ஒரு பொருளின் விலையில் ஏற்படும் விகிதாச்சார மாற்றத்திற்கும் அதன் காரணமாக தேவையில் ஏற்படும் விகிதாச்சார மாற்றத்திற்கான விகிதமே தேவை நெகிழ்ச்சி எனப்படும். கணிதக் குறியீடுகளில்

ed = (P / x) (dx / dp)

தேவைச் சார்பு Q = a - bP எனில் 

ed = (dQ / dP) (P/Q)

எடுத்துக்காட்டு: 12.21 

தேவைச்சார்பு x =100 /P என்கிறபோது விலையைப்பொருத்து தேவை நெகிழ்ச்சி e யை விலை P = 2 ஆக இருக்கும் போது காண்க.

தீர்வு :

x = 100 / P = 100 P-1 என தரப்பட்டுள்ளது

குறிப்பு:

அளிப்பு சார்பை பயன்படுத்தி அளிப்பு நெகிழ்ச்சிக்கெழு மதிப்பைக் காணலாம்.

∴ dx / dp = 100 (-1) P-1-1

= 100(-1)P-2

= -100(P-2)

= -100 / P2

P = 2 என்றால்

dx / dp = -100 / 4 = -25 மற்றும் x = 100 / 2 = 50

சூத்திரத்தில் மதிப்புகளைப் பிரதியிட

ed = Pdx / xdp = (2 / 50) ( -100/4) = -200 / 200 = -1

ed = -1