காந்தவியல் மற்றும் மின்னோட்டத்தின் காந்தவிளைவுகள்: கணக்குகள்

IV. கணக்குகள்:

1. காந்தத்திருப்புத்திறன் கொண்ட சட்ட காந்தமொன்று நான்கு துண்டுகளாக வெட்டப்படுகிறது. அதாவது முதலில் காந்தத்தின் அச்சைப்பொறுத்து இரண்டு துண்டுகளாகவும் பின்பு ஒவ்வொரு துண்டும், மேலும் இரண்டு துண்டுகளாகவும் வெட்டப்படுகின்றன. ஒவ்வொரு துண்டின் காந்தத் திருப்புத்திறனையும் காண்க.

தீர்வு

சட்ட காந்தம் ஒன்றை 'l' நீளத்தில் வெட்டும் போது,

புதிய முனை வலிமை M' = m /4

புதிய நீளம் l'= l

காந்தத் திருப்புத்திறன், M'= [m/4] × l

= ml / 4 

= M / 4

M புதியது = M / 4

2. நீள் அடர்த்தி 0.2 g m−1 கொண்ட கடத்தி ஒன்று படத்தில் காட்டியுள்ளவாறு இரண்டு நெகிழ்ச்சித்தன்மை கொண்ட கம்பிகளினால் தொங்கவிடப்பட்டுள்ளது. தாளுக்கு உள்ளே செல்லும் திசையில் 1T வலிமை கொண்ட காந்தப்புலத்திற்குள் இவ்வமைப்பு வைக்கப்படும்போது, கடத்தி தொங்க விடப்பட்டுள்ள கம்பிகளின் இழுவிசை சுழியாகிறது எனில், கடத்தியின் வழியே பாயும் மின்னோட்டம் மற்றும் மின்னோட்டம் பாயும் திசை ஆகிவற்றைக் காண்க. g = 10 m s−2 எனக் கருதுக.

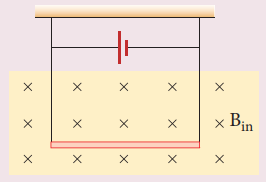
(விடை : 2 mA)

3. குறுக்கு வெட்டுப்பரப்பு 0.1 cm2 கொண்ட வட்டக்கம்பிச்சுருள் ஒன்று 0.2 T வலிமை கொண்ட சீரான காந்தப்புலம் ஒன்றினுள் வைக்கப்பட்டுள்ளது. கம்பிச்சுருள் வழியே பாயும் மின்னோட்டம் 3A மேலும் கம்பிச்சுருளின் பரப்பு காந்தப்புலத்திற்கு செங்குத்தாக உள்ளபோது பின்வருவனவற்றைக் காண்க. 

(அ) கம்பிச் சுருளின் மீது செயல்படும் மொத்த திருப்புவிசை 

(ஆ) கம்பிச் சுருளின் மீது செயல்படும் மொத்த விசை

(இ) காந்தப்புலத்தினால் கம்பிச்சுருளில் உள்ள ஒவ்வொரு எலக்ட்ரானின் மீதும் செயல்படும் சராசரி விசை (கம்பிச்சுருள் செய்யப்பட்டுள்ள பொருளின் கட்டுறா எலக்ட்ரான்அடர்த்தி 1028 m−3 எனக் கொள்க). 

தீர்வு: 

N =1

A = 0.1 × 10−4m2

B = 0.2T 

I = 3A

θ = 0°

(காந்தப்புலத்திற்கு செங்குத்தாக உள்ளது)

n = 1028m−3

அ) திருப்பு விசை, τ = NIBsin θ

=1 × 3 × 0.2 × 0.1 × 10−4 × sin 0°

திருப்பு விசை = 0

ஆ) கம்பிச் சுருளின் மீது செயல்படும் மொத்த விசை சுழியாகும்.

இ) எலக்ட்ரான்கள் மீது செயல்படும் சராசரி விசை

= 6 × 10−28 × 104

சராசரி விசை = 6 ×10−24

= 0.6 ×10−23 N

(விடை : (அ) சுழி (ஆ) சுழி (இ) 0.6 ×10−23 N)

4. 0.8T வலிமை கொண்ட சீரான காந்தப்புலம் ஒன்றினுள் சட்ட காந்தமானது வைக்கப்பட்டுள்ளது. சட்டகாந்தம் காந்தப்புலத்துடன் 30° கோணத்தை ஏற்படுத்தும்படி ஒருங்கமைந்து, 0.2 Nm திருப்புவிசையை உணர்கிறதெனில் பின்வருவனவற்றைக் கணக்கிடுக. 

i) சட்ட காந்தத்தின் காந்தத்திருப்புத்திறன் 

ii) மிகவும் உறுதியான ஒருங்கமைப்பில் (Most stable configuration) இருந்து மிகவும் உறுதியற்ற (Most unstable configuration) ஒருங்கமைப்பிற்கு சட்ட காந்தத்தை நகர்த்துவதற்கு அளிக்கப்படும் விசையினால் செய்யப்பட்ட வேலை மற்றும் செலுத்தப்படும் காந்தப்புலத்தால் செய்யப்படும் வேலை ஆகியவற்றைக் கணக்கிடுக. 

தீர்வு: 

i) B = 0.8 T

θ = 30o

τ = 0.2 Nm

τ = Pm B sin θ

ii)W = Uf – Ui

Uf = μB cos 180° 

Ui = − μB cos 0°

∴ W = μB cos 180°− (− μB cos 0°)

= μB + μB = 2 μB

W = 2 μB

= 2ρm B

= 2 × 0.5 × 0.8

= 0.85 J மற்றும் Wகாந்தப்புலம் = − 0.85 J

(விடை : (i) 0.5 A m2 (ii) W = 0.8 J மற்றும் Wகாந்தப்புலம் = − 0.8 J)

5. 100g நிறையும் 20 cm ஆரமும் கொண்ட மின்கடத்தா கோளத்தைச் சுற்றி தட்டையான கம்பியைக் கொண்டு 5 சுற்றுக்கள் இறுக்கமாக சுற்றப்படுகிறது. கம்பிச்சுருளின் தளம் சாய்தளத்திற்கு இணையாக இருக்கும்படி கோளம் சாய்தளத்தின் மீது வைக்கப்பட்டுள்ளது. 0.5T வலிமை கொண்ட காந்தப்புலம் செங்குத்தாக மேல் நோக்கிச் செயல்படும்படி அமைக்கப்பட்டு கம்பிச்சுருள் வழியே மின்னோட்டம் செலுத்தப்படுகிறது. எவ்வளவு மின்னோட்டத்தை கம்பிச்சுருள் வழியே செலுத்தினால் கோளம் சாய்தளத்தின் மீது சமநிலையில் நிற்கும்.

தீர்வு:

கோளம் சமநிலையில் உள்ளது.

fS − Mg sin θ = 0 ................ (1) 

கோளம் சுழற்சி சமநிலையில் உள்ளது.

திருப்பு விசை = μ B sin θ (காந்தப்புலத்தினால் உருவானது)

உராய்வு விசை= fS R

R = கோளத்தின் ஆரம்

fS R − μ B sin θ = 0 ............... (2)

சமன்பாடு 1 ஐ 2 இல் பிரதியிட்டால்

fS = mg sin θ

∴ mg sin θ R − μ B sin θ = 0

mg sin θ R = μ B sin θ

μ B = mgR ............... (3)

μ = NIA

μ = NIπr2 ............... (4)

NIπr2 B = mgR

m = 100g = 100 × 10− 3 kg

= 0.1 kg

R = 20cm = 0.2 m

B = 0.5 T

N = 5 சுழற்சி

g = 10m / s2

= 1 / 0.5 π

I = 2/π A

(விடை : 2/π A)

6. 1.5 A மின்னோட்டம் பாயும் சதுர வடிவ கடத்தியின் மையத்தில் ஏற்படும் காந்தப்புலத்தைக் காண்க. சதுரத்தின் ஒவ்வொரு பக்கங்களின் நீளமும் 50 cm ஆகும்.

(விடை: 3.4 × 10−6 T)