நிகழ்தகவின் சில அடிப்படைத் தேற்றங்கள்

நிகழ்தகவின் சில அடிப்படைத் தேற்றங்கள்

இதுவரை தீர்க்கப்பட்ட கணக்குகள்யாவும் ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகளுடன் தொடர்புடையவை. அதாவது P(Aஅல்லது B) = P(A∪B) = P(A) + P(B) என்ற சூத்திரம் பயன்படுத்தப்பட்டது. ஆனால் நிகழ்வுகள் ஒன்றையொன்று விலக்கா நிகழ்ச்சிகள் எனில் (A∩B) இருமுறை கணக்கில் எடுத்துக் கொள்ளப்படுகிறது. நிகழ்ச்சிகள் ஒன்றையொன்று விலக்கா நிகழ்ச்சிக்குத் தனிச் சூத்திரம் உள்ளது.

நிகழ்தகவியலில் உள்ள எல்லாத் தேற்றங்களும் நேரடியாகவோ அல்லது மறைமுகமாகவோ, நிகழ்தகவின் அடிப்படைக் கொள்கைகளைப் பயன்படுத்தித் தருவிக்கப்படுகின்றன. நிகழ்தகவின் சில அடிப்படைத் தேற்றங்களை இங்கு தருவிப்போம்.

தேற்றம் 12.3

நடக்க இயலா நிகழ்ச்சியின் நிகழ்தகவு பூச்சியம் ஆகும். அதாவது,

P(Ø) = 0

நிரூபணம்

நடக்கவியலா நிகழ்ச்சி Ø ல் கூறுபுள்ளி கிடையாது. எனவே, S ∪ Ø =S

P(S ∪ Ø)= P(S)

P(S) + P(Ø) = P(S) (S மற்றும் Ø ஆகியவை ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகளாகும்)

P(Ø) = 0

எடுத்துக்காட்டு 12.12

ஒரு பகடையை உருட்டிவிடும்போது 7 கிடைப்பதற்கான நிகழ்தகவைக் காண்க.

தீர்வு

7 கிடைப்பதற்கான நிகழ்ச்சி நடக்கவியலா நிகழ்ச்சி ஆகும். எனவே P (7 கிடைக்கப்பெற) = 0.

தேற்றம் 12.4

Ā என்பது A என்ற நிகழ்வின் நிரப்பியானால்,

P(Ā) = 1− P(A)

நிரூபணம்

S என்பது கூறுவெளி எனில்

A∪Ā = S

P(A ∪Ā) = P(S)

P(A) + P(Ā) = P(S) (ஏனெனில் A மற்றும் Ā ஒன்றையொன்று விலக்கும் தன்மையுடையதால்)

P(Ā) = 1- P(A) அல்லது P(A) = 1-P(Ā)

எடுத்துக்காட்டு 12.13

ஒன்பது நாணயங்கள் ஒரு முறை சுண்டப்படும்போது குறைந்தது இரண்டு தலைகள் கிடைப்பதற்கான நிகழ்தகவைக் காண்க.

தீர்வு

S என்பது கூறுவெளி என்க. A என்பது குறைந்தது இரண்டு தலைகள் கிடைப்பதற்கான நிகழ்ச்சி என்க. Ā என்பது அதிகபட்சமாக ஒரு தலை கிடைக்கும் நிகழ்ச்சிகள் ஆகும்.

தேற்றம் 12.5

A, B என்பன ஏதேனும் இரு நிகழ்ச்சிகள் மற்றும் என்பது B -ன் நிரப்பியெனில்

நிரூபணம்

படத்திலிருந்து தெளிவாக

மற்றும் A∩B ஒன்றுக்கொன்று விலக்கும் நிகழ்ச்சிகளாக இருப்பதால்

தேற்றம் 12.6 (நிகழ்தகவின் கூட்டல் தேற்றம்)

A, B என்பன ஏதேனும் இரு நிகழ்ச்சிகள் எனில்

P(A ∪ B) = P(A) + P(B) − P(A∩B)

நிரூபணம்

= [P(A) – P (A∩B)] + P(B)

எனவே P(A∪B) = P(A) + P(B) – P(A∩B)

குறிப்பு 12.4

மேற்கண்ட தேற்றத்தை மூன்று நிகழ்ச்சிகளுக்கும் விரிவுபடுத்தலாம்.

(i) P(A∪ B∪ C) = {P(A) + P(B) + P(C)} - {P(A∩B) + P(B∩C) + P(C∩A)} + P(A∩B∩C)

எடுத்துக்காட்டு 12.14

P(A) = 0.52, P(B) = 0.43, மற்றும் P (A∩B) = 0.24, எனில்

எடுத்துக்காட்டு 12.15

போட்டித் தேர்வுகளுக்கு தயாராகும் ஒரு பெண்ணிற்கு மாநில அரசுப் பணி கிடைப்பதற்கான நிகழ்தகவு 0.12, மற்றும் மத்திய அரசு வேலை கிடைப்பதற்கான நிகழ்தகவு 0.25, மற்றும் இரு பணிகளும் கிடைப்பதற்கான நிகழ்தகவு 0.07 எனில் (i) இரண்டில் ஒரு பணி கிடைப்பதற்கான நிகழ்தகவு (ii) ஒரே ஒரு பணி மட்டுமே கிடைப்பதற்கான நிகழ்தகவு காண்க. 

தீர்வு

I என்பது மாநில அரசு பணி கிடைப்பதற்கான நிகழ்ச்சி என்க. C என்பது மத்திய அரசு பணி கிடைப்பதற்கான நிகழ்ச்சி என்க.

கொடுக்கப்பட்டவை P(I) = 0.12, P(C) = 0.25, மற்றும் P(I∩C) = 0.07

(i) P (இரண்டிலொரு பணி கிடைப்பதற்கான) = P(I அல்லது C) = P(I∪ C)

= P(I) + P(C) - P(I∩C)

= 0.12 + 0.25 - 0.07 = 0.30

(ii) P(ஒரே ஒரு பணி கிடைப்பதற்கான) = P[I மட்டும் அல்லது C மட்டும்].

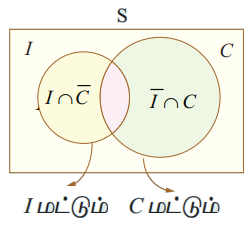
= {P(I) – P(I∩C)} + {P(C) – P(I∩C)}

= {0.12 − 0.07} + {0.25 − 0.07}

= 0.23.