பயிற்சி 1.3

பயிற்சி 1.3

பல்வகைத் திறனறிப் பயிற்சிக் கணக்குகள்

1. 2–ஐ விடப் பெரிய இரட்டை எண் ஒவ்வொன்றையும் இரண்டு பகா எண்களின் கூடுதலாக வெளிப்படுத்தலாம். இதனை, 16 வரையுள்ள ஒவ்வோர் இரட்டை எண்ணுக்கும் சரிபார்க்க.

தீர்வு : 

2 ஐ விடப் பெரிய 16 வரையிலான இரட்டை எண்கள் 4, 6, 8, 10, 12, 14

4 = 2 + 2 

6 = 3 + 3 

8 = 3 + 5 

10 = 5 + 5 அல்லது 3 + 7 

12 = 5 + 7 

14 = 7 + 7 அல்ல து 3 + 11 

16 = 5 + 11 அல்ல து 3 + 13.

2. 173, ஒரு பகா எண்ணா? ஏன்?

தீர்வு : 

ஆம் 173 ஒரு பகா எண்

ஏனெனில் இதன் காரணிகள் 1 மற்றும் 173. 

2 காரணிகளை மட்டுமே பெற்றுள்ளதால் 173 ஒரு பகா எண்.

3. n = 2 முதல் 8 வரை உள்ள எந்த எண்களுக்கு, 2n–1 ஆனது, ஒரு பகா எண் ஆகும்?

தீர்வு :

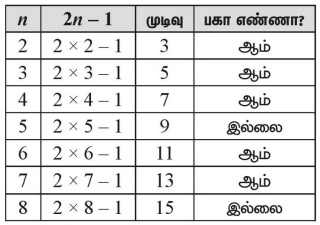
n = 2, 3, 4, 6, 7 ஆகிய எண்களுக்கு 2n – 1 ஒரு பகா எண்

4. பின்வரும் கூற்றுகளைக் காரணத்தோடு விளக்குக.

அ) ஓர் எண் 3 ஆல் வகுபடும் எனில், அவ்வெண் 9 ஆல் வகுபடும்.

ஆ) ஓர் எண் 12 ஆல் வகுபடும் எனில், அவ்வெண் 6 ஆல் வகுபடும்.

தீர்வு : 

அ) தவறு.

3 இன் மடங்குகள் அனைத்தும் 3 ஆல் வகுபடும் ஆனால் 9 இன் மடங்குளைத் தவிர்த்த 3 ன் மடங்குகள் 9 ஆல் வகுபடுவதில்லை .

 எ.கா. 3, 6, 12, 15, .... 

ஆ) சரி. 

ஏனெனில் 12 ஆனது 6 இன் மடங்கு. 

எனவே 12 ஆல் வகுபடும் எண்கள் 6 ஆல் வகுபடும்.

எ.கா. 12, 24, 36, 48, .........

5. கீழ்க்காணும் கூற்றுகளுக்கு ஏற்ப A இன் மதிப்பைக் காண்க

(i) 2 ஆல் வகுபடும் மிகப்பெரிய ஈரிலக்க எண் 9A ஆகும்.

(ii) 3 ஆல் வகுபடும் மிகச்சிறிய எண் 567A ஆகும்.

(iii) 6 ஆல் வகுபடும் மிகப்பெரிய மூன்றிலக்க எண் 9A6 ஆகும்.

(iv) 4 மற்றும் 9 ஆல் வகுபடும் எண் A08 ஆகும்.

(v) 11 ஆல் வகுபடும் எண் 225A85 ஆகும்.

தீர்வு : 

(i) ஒரு எண் இரட்டை எண் எனில் அது 2ஆல் வகுபடும். மிகப்பெரிய ஈரிலக்க இரட்டை எண் 98 ஃ A = 8. 

(ii) ஒரு எண் 3 ஆல் வகுப்படுமெனில், அதன் இலக்கங்களின் கூடுதல் 3 ஆல் வகுபடும்.

5 +  6 + 7 + A = 18 + A. 

18 ஆனது 3 ஆல் வகுபடும்.

ஃ கூட்ட வேண்டிய மிகச்சிறிய எண் = A = 0 

(iii) ஒரு எண் 6 ஆல் வகுபடுமெனில் அவ்வெண் 2 மற்றும் 3 ஆல் வகுபடும்.

9A6 ஒரு இரட்டை எண். எனவே 2 ஆல் வகுப்படும். 

3 ஆல் வகுபட இலக்கங்களின் கூடுதல் = 9 + A + 6

= 15 + A ஆனது 3 ஆல் வகுபட வேண்டும். 

15 ஆனது 3 ஆல் வகுபடும். எனவே A ஆனது 3 ஆல் வகுபடும் ஒரிலக்க பெரிய எண்.

ஃ A = 9.

(iv) A=1

(v) A=8

6. 4 மற்றும் 6 ஆல் வகுபடும் எண்கள் 24 ஆல் வகுபடும். இந்தக் கூற்றை ஓர் எடுத்துக்காட்டுடன் சரிபார்க்க.

விடை : 

தவறு 12 ஆனது 4 மற்றும் 6 ஆல் வகுபடும். ஆனால் 24 ஆல் வகுபடாது.

7. எவையேனும் இரு அடுத்தடுத்த ஒற்றை எண்களின் கூடுதலானது 4 ஆல் வகுபடும். இந்தக் கூற்றை ஓர் எடுத்துக்காட்டுடன் மெய்ப்பிக்க.

விடை : 

சரி 17 + 19 = 36 என்பது 4 ஆல் வகுபடும்.

8. 1 மீ 20 செ.மீ, 3 மீ 60 செ.மீ மற்றும் 4 மீ அளவுகளைக் கொண்ட கயிறுகளின் நீளங்களைச் சரியாக அளக்கப் பயன்படும் கயிற்றின் அதிகபட்ச நீளம் என்ன?

விடை : 

1மீ 20 செ.மீ = 120 செ.மீ

3மீ 60 செ.மீ= 360 செ.மீ

4 மீ = 400 செ.மீ 

இது மீ.பெ.கா தொடர்பான கணக்கு ஆகும். ஆகவே, நாம் 120, 360, 400 ஆகியவற்றின் மீ.பெ.காவைக் காண வேண்டும்

120 = 2 × 2 × 2 × 3 × 5 

360 = 2 × 2 × 2 × 3 × 3 × 5 

400 = 2 × 2 × 2 × 2 × 5 × 5 

மீ.பெ.கா = 2 × 2 × 2 × 5 

மீ.பெ.கா = 40

கயிற்றின் அதிகளவு நீளம் = 40 செ.மீ .

மேற்சிந்தனைக் கணக்குகள்

9. மூன்று பகா எண்களின் கூடுதல் 80. அவற்றுள் இரு எண்களின் வேறுபாடு 4 எனில், அந்த எண்களைக் காண்க.

விடை: 

பகா எண்கள் 2, 37, 41 

கூடுதல் 2 + 37 + 4 = 80

வித்தியாசம் 41– 37=4

10. 10 முதல் 20 வரையுள்ள அனைத்துப் பகா எண்களின் கூடுதலானது அனைத்து ஓரிலக்க எண்களால் வகுபடுமா என ஆராய்க.

விடை: 

10 க்கும் 20 க்கும் இடையே உள்ள பகா எண்கள் 11, 13, 17, 19

கூடுதல் 11 + 13 + 17 + 19 = 60 

60 ஆனது 1, 2, 3, 4, 5, 6ஆல் வகுபடும்.

11. 1 இலிருந்து 9 வரையிலான அனைத்து எண்களாலும் வகுபடும் மிகச்சிறிய எண்ணைக் காண்க.

விடை : 2520

12. மூன்று தொடர்ச்சியான எண்களின் பெருக்கற்பலன் எப்போதும் 6 ஆல் வகுபடும் என்பதை ஓர் எடுத்துக்காட்டுடன் மெய்ப்பிக்க.

விடை : ஆம் 

2 × 3 × 4 = 24 ஆனது 6 ஆல் வகுபடும்.

13. மலர்விழி, கார்த்திகா மற்றும் கண்ணகி ஆகிய மூவரும் ஒரே கிராமத்தைச் சேர்ந்த தோழிகள். இவர்கள் வெவ்வேறு இடங்களில் வேலை செய்கின்றனர். மலர்விழி 5 நாட்களுக்கு ஒரு முறையும், கார்த்திகா மற்றும் கண்ணகி முறையே 6 மற்றும் 10 நாட்களுக்கு ஒரு முறையும், அவர்தம் வீடுகளுக்கு வந்து செல்வர். அவர்கள் மூவரும், அக்டோபர் மாதம் முதல் நாள் ஒன்றாகச் சந்தித்தார்கள் எனில், மீண்டும் அவர்கள் எப்போது ஒன்றாகச் சந்திப்பார்கள்?

விடை: 

இது மீ.சி.ம தொடர்பான கணக்கு ஆகும். ஆகவே, நாம் 5, 6 மற்றும் 10 ஆகியவற்றின் மீ.சி.மவைக் காண வேண்டும்?

மீ.சி.ம = 5 × 2 × 1 × 3 × 1 = 30 

எனவே, மீண்டும் அவர்கள் 30 நாள்களுக்கு ஒரு முறை சந்திப்பார்கள்.

14. 108 தளங்களைக் கொண்ட ஓர் அடுக்கு மாடிக் குடியிருப்பில் A மற்றும் B என இரண்டு மின்தூக்கிகள் உள்ளன. இரண்டு மின் தூக்கிகளும் தரை தளத்திலிருந்து தொடங்கி, முறையே ஒவ்வொரு 3வது மற்றும் 5வது தளத்தில் நின்று செல்கின்றன. எந்தெந்தத் தளங்களில், இந்த இரண்டு மின்தூக்கிகளும் ஒன்றாக நின்று செல்லும்?

விடை : 

3 மற்றும் 5ன் மீசிம = 3 × 5 = 15 

எனவே, மின்தூக்கியானது 15,30, 45, 60,75, 90 மற்றும் 105 ஆகிய தளங்களில் நின்று செல்லும்.

15. இரண்டு ஈரிலக்க எண்களின் பெருக்கற்பலன் 300 மற்றும் அவற்றின் மீ.பெ.கா. 5 எனில், அவ்வெண்கள் யாவை?

விடை: 

15 × 20 = 300

15 மற்றும் 20ன் மீபெகா 5 

அவ்வெண்கள் = 15 மற்றும் 20

16. 564872 என்ற எண்ணானது 88 ஆல் வகுபடுமா என ஆராய்க. (8 மற்றும் 11 இன் வகுபடுந்தன்மை விதிகளைப் பயன்படுத்தலாம்!)

விடை : 564872

8 ஆல் வகுபடுந்தன்மை 

564872–8 ஆல் வகுபடும் 

564872–11 ஆல் வகுபடுந்தன்மை 

5 + 4 + 7 = 16 

6 + 8 + 2 = 16 

16 – 16 = 0

ஆம். ஏனெனில் அது 8 மற்றும் 11 ஆல் வகுபடுவதால் 88 ஆல் வகுபடும்.

17. வில்சன், மதன் மற்றும் குணசேகரன் ஆகியோர் ஒரு வட்ட வடிவிலான ஓடுபாதையின் ஒரு சுற்றை முறையே 10, 15 மற்றும் 20 நிமிடங்களில் சுற்றி முடிக்கின்றனர். அவர்கள் தொடக்கப் புள்ளியில் காலை 7 மணிக்கு ஒன்றாகச் சுற்றத் தொடங்கினால், அவர்கள் மீண்டும் எப்போது தொடக்கப் புள்ளியில் ஒன்றாகச் சந்திப்பார்கள்?

விடை :

இது மீசிம தொடர்பான கணக்கு ஆகும். ஆகவே, நாம் 10, 15 மற்றும் 20 ஆகியவற்றின் மீ.சிம வைக் காண வேண்டும். 

10, 15, 20 இன் மீசிம

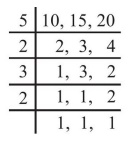
மீசிம = 5 × 2 × 1 × 3 × 2 = 60 நிமிடங்கள் 

எனவே, அவர்கள் மீண்டும் 60 நிமிடங்களுக்குப் பிறகு, காலை 8 மணிக்கு தொடக்கப் புள்ளியில் ஒன்றாகச் சந்திப்பார்கள்.

உங்களுக்குத் தெரியுமா?

இரு எண்களில், ஓர் எண்ணின் காரணிகளின் (அந்த எண்ணைத் தவிர்த்து) கூடுதலானது மற்றோர் எண்ணைத் தரும் எனில், அவை 'இணக்கமான எண்கள்' எனப்படும்.

220 மற்றும் 284 ஆகிய எண்கள்'இணக்கமான எண்கள்' ஆகும். ஏனெனில், 220 இன் காரணிகளின் (220–ஐத் தவிர) கூடுதலான 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 ஆகும். மேலும், 284 இன் காரணிகளின் (284–ஐத் தவிர) கூடுதலான 1 + 2 + 4 + 71 + 142 = 220 ஆகும்.

1184 மற்றும் 1210 ஆகிய எண்கள் இணக்கமான எண்களா என ஆராய்க.