அணிகளின் பயன்பாடுகள் : நேரியச் சமன்பாடுகளின் தொகுப்பிற்கான தீர்வு காணுதல் (Applications of Matrices: Solving System of Linear Equations)

எடுத்துக்காட்டு 1.22

பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பை நேர்மாறு அணி காணல் முறையை பயன்படுத்தி தீர்க்க:

5x + 2y = 3, 3x + 2y = 5.

தீர்வு

தொகுப்பின் அணி வடிவம் AX = B, இங்கு

|A| =   = 10 – 6 = 4 ≠ 0. எனவே A−1 காண இயலும். மற்றும் A−1 =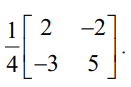  

X = A−1B என்ற சூத்திரத்தைப் பயன்படுத்தக் கிடைப்பது

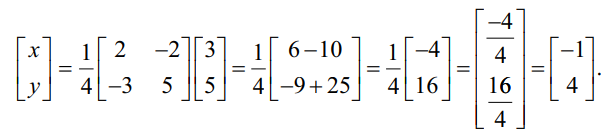
எனவே தீர்வானது (x = −1, y = 4).

எடுத்துக்காட்டு 1.23

பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பை நேர்மாறு அணி காணல் முறையை பயன்படுத்தி தீர்க்க:

2x1 + 3x2 + 3x3 = 5, x1 − 2x2 + x3 = −4, 3x1 – x2 − 2x3 = 3.

தீர்வு

தொகுப்பின் அணி வடிவம் AX = B.

எனவே A−1 காண இயலும் மற்றும்

X = A−1B என்ற சூத்திரத்தைப் பயன்படுத்தக் கிடைப்பது

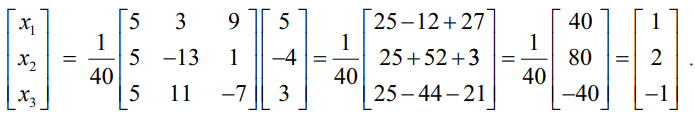
எனவே தீர்வானது (x1 = 1, x2 = 2, x3 = −1).

எடுத்துக்காட்டு 1.24

எனில் பெருக்கற்பலன் AB மற்றும் BA காண்க.

இதன் மூலம் x – y + z = 4, x − 2y − 2z = 9, 2x + y + 3z = 1 என்ற நேரியச்  சமன்பாட்டுத் தொகுப்பைத் தீர்க்கவும்.

தீர்வு

எனவே நாம் பெறுவது AB = BA = 8I3. அதாவது, ( (1/8) A) B  = B ( (1/8) A) = I3. எனவே, B−1 = (1/8) A. 

கொடுத்துள்ள நேரியச் சமன்பாட்டுத் தொகுப்பை அணி வடிவில் எழுதக் கிடைப்பது

எனவே தீர்வானது ( x = 3, y = −2, z = −1).

எடுத்துக்காட்டு 1.25

x1 − x2 = 3, 2x1 + 3x2 + 4x3 = 17, x2 + 2x3 = 7 என்ற நேரியச் சமன்பாடுகளின் தொகுப்பைத் தீர்க்கவும்.

தீர்வு

பின்வரும் அணிக்கோவைகளின் மதிப்பை முதலில் காண்போம்.

எனவே தீர்வானது (x1 = 2, x2 = −1, x3 = 4).

எடுத்துக்காட்டு 1.26

T20 ஆட்டமொன்றில் கடைசி ஓவரில் 1 பந்து மட்டும் வீசப்பட வேண்டிய நிலையில் ஓர் அணியானது 6 ரன்கள் (ஓட்டங்கள்) பெற்றால் மட்டுமே வெற்றி பெறும் நிலையில் இருந்தது. கடைசி பந்து மட்டையருக்கு வீசப்பட்டது. அவர் அதனை மிக உயரம் செல்லுமாறு அடிக்கிறார். பந்தானது செங்குத்து தளத்தில் சென்ற பாதை அத்தளத்தில் y = ax2 + bx + c என்ற சமன்பாட்டின்படி உள்ளது. பந்தானது (10,8), (20,16), (40,22) என்ற புள்ளிகள் வழியாகச் செல்கிறது எனில் அவ்வணியானது ஆட்டத்தை வென்றதா என்பதை முடிவு செய்யலாமா? உனது விடையினை கிராமர் விதியைக் கொண்டு நியாயப்படுத்துக. (எல்லா தொலைவுகளும் மீட்டர் அளவில் உள்ளன. பந்து சென்ற பாதையின் தளமானது மிகத்தொலைவில் உள்ள எல்லைக் கோட்டினை (70,0) என்ற புள்ளியில் சந்திக்கும்)

தீர்வு

y = ax2 + bx + c என்ற பாதையானது (10,8), (20,16), (40,22) என்ற புள்ளிகள் வழிச் செல்கிறது. ஆதலால் 100a + 10b + c = 8,400a + 20b + c = 16,1600a + 40b + c = 22 என்ற சமன்பாடுகள் கிடைக்கின்றன. கிராமரின் விதியை பயன்படுத்த பின்வருவனவற்றைக் காண்போம்.

x = 70 எனில் y = 6 எனக் கிடைக்கிறது. எனவே பந்தானது எல்லைக்கோட்டிற்கு நேர் மேலாக 6 மீ உயரத்தில் செல்கிறது மற்றும் எல்லைக் கோட்டின் அருகில் உள்ள ஆட்டக்காரர் எகிறிக் குதித்துப் பிடிக்க முயன்றாலும் அவரால் அப்பந்தினைப் பிடிக்க இயலாது. எனவே அப்பந்து மிகப்பெரிய 6 ஆகச் சென்றது மற்றும் அவ்வணி ஆட்டத்தினை வென்றது.

எடுத்துக்காட்டு 1.27

பின்வரும் நேரியச் சமன்பாட்டுத் தொகுப்பை காஸ்ஸியன் நீக்கல் முறையில் தீர்க்க: 

4x + 3y + 6z = 25, x + 5y + 7z = 13, 2x + 9y + z = 1.

தீர்வு

விரிவுபடுத்தப்பட்ட அணியை ஏறுபடிவ வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது,

ஏறுபடிவத்திலிருந்து கிடைக்கும் சமமான சமன்பாடுகளின் தொகுப்பானது

x + 5y + 7z = 13,    ... (1)

17y + 22z = 27,     ... (2)

199z = 398.         ... (3)

(3)−லிருந்து நாம் பெறுவது z = 398 / 199 = 2.

z = 2 என (2) −ல் பிரதியிடக் கிடைப்பது y = (27 – (22 × 2)) / 17 = −17 / 17 = −1.

z = 2 மற்றும் y = −1 என (1)−ல் பிரதியிடக் கிடைப்பது x = 13 – 5 × (−1) −7 × 2 = 4.

எனவே தீர்வானது (x = 4, y = −1, z = 2).

குறிப்பு: கடைசி சமன்பாட்டிலிருந்து முதல் சமன்பாட்டிற்கு மேலே உள்ள முறையானது பின்னோக்கி பிரதியிடல் முறை என அழைக்கப்படுகிறது.

எடுத்துக்காட்டு 1.28

ஒரு ராக்கெட்டின் மேல் நோக்கிய வேகம் t நேரத்தில் தோராயமாக v(t) = at2  + bt + c என்றவாறு உள்ளது. இங்கு 0 ≤ t ≤ 100 மற்றும் a, b, c என்பன மாறிலிகள். ராக்கெட்டின் வேகம் t = 3, t = 6, மற்றும் t = 9 வினாடிகளில் முறையே 64, 133, மற்றும் 208 மைல்கள் / வினாடி எனில் t = 15 வினாடியில் அதன் வேகத்தைக் காண்க. (காஸ்ஸியன் நீக்கல் முறையை பயன்படுத்துக).

தீர்வு

v(3) = 64, v(6) = 133 மற்றும் v(9) = 208. ஆதலால் பின்வரும் நேரிய சமன்பாட்டுத் தொகுப்பைப் பெறுகிறோம்.

9a + 3b + c = 64,

36a + 6b + c = 133,

81a + 9b + c = 208.

மேல் உள்ள நேரியச் சமன்பாட்டுத் தொகுப்பை காஸ்ஸியன் நீக்கல் முறையில் தீர்க்க உள்ளோம். விரிவுபடுத்தப்பட்ட அணியை நிரை − ஏறுபடி வடிவத்திற்கு தொடக்கநிலை நிரை உருமாற்றங்கள் செயல்படுவதன் மூலம் நாம் பெறுவது,

ஏறுபடி வடிவத்திலிருந்து கிடைக்கும் சமான சமன்பாடுகள்

9a + 3b + c = 64, 2b + c = 41, c = 1.

பின்னோக்கிப் பிரதியிடல் மூலம் நமக்குக் கிடைப்பது

c = 1, b = (41 − c) / 2 = (41 − 1) / 2 = 20, a = (64 – 3b − c) / 9 = (64 – 60 – 1) / 9 = 1 / 3.

ஆதலால் v(t) = (1 / 3)t2 + 20t + 1.

எனவே, v(15) = (1 / 3) (225) + 20 (15) + 1 = 75 + 300 + 1 = 376 மைல்கள் / வினாடி.