Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ | Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Cyclic Quadrilaterals) | 9th Maths : UNIT 4 : Geometry
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 4 : Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Cyclic Quadrilaterals)
Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Cyclic Quadrilaterals)
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»Ђ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я«ЙЯ««Я»Ї. Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я«┐Я«цЯ«┐Я«»Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЄЯ«»Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.

Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї ABCDЯ«љ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«Ћ. Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«јЯ«цЯ«┐Я«░Я»єЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ»ѕЯ«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«Е Я««Я»єЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я»ЂЯ«ЕЯ»ѕЯ«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я»Ї O Я«ЅЯ«ЪЯ«ЕЯ»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. OA, OB, OC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї OD Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«єЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«░Я»ЂЯ«џЯ««Я«фЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї OAB, OBC, OCD Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ODA Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я»Ї O Я«хЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 360┬░
Я«њЯ«хЯ»ЇЯ«хЯ»ІЯ«░Я»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«фЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 180┬░. Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ (Я«фЯ«ЪЯ««Я»Ї 4.77) Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ,

2 ├Ќ (Рѕа1 + Рѕа2 + Рѕа3 + Рѕа4) + Я««Я»ѕЯ«»Я««Я»Ї O Я«ЄЯ«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї = 4 ├Ќ 180┬░
2 ├Ќ (Рѕа1+Рѕа2+Рѕа3+Рѕа4) + 360┬░ = 720┬░
Я«ЄЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ, (Рѕа1+Рѕа2+Рѕа3+Рѕа4) = 180┬░.
Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ»Ђ,
(i) (Рѕа1+Рѕа2) + ( Рѕа3+Рѕа4) = 180┬░ (Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D Я«ЄЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї)
(ii) ( Рѕа1+Рѕа4) + ( Рѕа2+ Рѕа3) = 180┬░ (Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«ЄЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї)
Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е
:
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 12 Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ»ѕЯ«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 12Я«ЄЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я»Ї Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 12 Я«ЄЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕ Я«њЯ«░Я»Ђ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«џЯ»ІЯ«ЪЯ«┐ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ»ѕЯ«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Рѕњ 7
Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕ
9. O Я«хЯ»ѕ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«єЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ..
10. Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї A, B, C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D Я«љ Я«ЁЯ«цЯ«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї ABCD Я«љ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«ЪЯ««Я»Ї 4.78Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«фЯ»ІЯ«▓Я»Ї Я«фЯ»єЯ«»Я«░Я«┐Я«ЪЯ»ЂЯ«Ћ.

11. Я«фЯ«ЪЯ«┐ Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї ABCD Я«љЯ«фЯ»Ї Я«фЯ«ЪЯ«┐Я«»Я»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ.
12. Я«фЯ«ЪЯ««Я»Ї 4.79 Я«ЄЯ«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A, B, C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D Я«љ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ.

13. Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Рѕа1, Рѕа2, Рѕа3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕа4 Я«љЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї A, B, C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D Я«ЄЯ«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«ЪЯ««Я»Ї 4.80 Я«ЄЯ«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«њЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«Ћ.
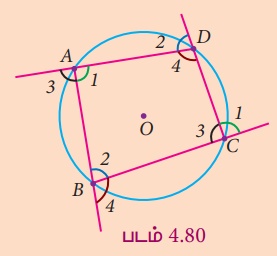
14. Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Рѕа1+ Рѕа3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕа2 + Рѕа4 Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«ЅЯ«▒Я»ЇЯ«▒Я»ЂЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«Ћ:
1. (i) РѕаA + РѕаC = _____
(ii) РѕаB+ РѕаD = _______
(iii) РѕаC + РѕаA = _____
(iv) РѕаD + РѕаB = _______
2. Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»єЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї _______.
3. Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ____.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.10
Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї PQRS Я«ЄЯ«▓Я»Ї РѕаPSR = 70┬░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаQPR = 40┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РѕаPRQ Я«љЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ (Я«фЯ«ЪЯ««Я»Ї 4.81 Я«љЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ).

Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї PQRS Я«ЄЯ«▓Я»Ї РѕаPSR = 70┬░ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ
РѕаPSR
+ РѕаPQR
= 180┬░ (Я«ЋЯ«ЙЯ«░Я«БЯ««Я»Ї
Я«ЋЯ»ѓЯ«▒Я»ЂЯ«Ћ РђдРђд.)
70┬░ + РѕаPQR
= 180┬░
РѕаPQR
= 180┬░ Рѕњ 70┬░
РѕаPQR
= 110┬░
РѕєPQR Я«ЄЯ«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ,
РѕаPQR + РѕаPRQ+ РѕаQPR = 180┬░ (Я«ЋЯ«ЙЯ«░Я«БЯ««Я»Ї Я«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋРђдРђдРђд)
110┬░ + РѕаPRQ + 40┬░ = 180┬░
РѕаPRQ
= 180┬░ Рѕњ 150┬░
РѕаPRQ
= 30┬░
Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (Exterior Angle of a Cyclic Quadrilateral)
Я«њЯ«░Я»Ђ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЈЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЂЯ««Я»Ї, Я«ЁЯ«цЯ«ЕЯ»ѕ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«ЪЯ»ЇЯ«џЯ«┐Я«»Я»ЂЯ««Я»Ї Я«хЯ»єЯ«│Я«┐Я«»Я»Є Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.

Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї ABCD Я«ЄЯ«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї AB Я«љ E Я«хЯ«░Я»ѕ Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«Ћ. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, РѕаABC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаCBE Я«єЯ«ЋЯ«┐Я«»Я«Е Я«еЯ»ЄЯ«░Я«┐Я«» Я«ЋЯ»ІЯ«БЯ«џЯ»Ї Я«џЯ»ІЯ«ЪЯ«┐Я«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 180┬░ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, РѕаABC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаADC Я«єЯ«ЋЯ«┐Я«»Я«Е Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ««Я»Ї 180┬░ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ, РѕаABC + РѕаCBE = РѕаABC + РѕаADC Я«єЯ«ЋЯ«хЯ»Є РѕаCBE = РѕаADC . Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 13 Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я»єЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї.
Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ»ІЯ«цЯ«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї
1. Я«њЯ«░Я»Ђ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«џЯ»ІЯ«ЪЯ«┐ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ»ѕ Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї РђдРђдРђд.. Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
2. Я«еЯ«ЙЯ«БЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї РђдРђдРђд..
3. Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я«ЅЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«│Я«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЅЯ«│Я»ЇЯ«│Я»єЯ«цЯ«┐Я«░Я»Ї Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ РђдРђдРђд..
4. Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї РђдРђдРђд..
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.11
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї x┬░
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y┬░
Я«ЄЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.

Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«хЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐,
Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ, y┬░ =100┬░ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї,
x┬░ + 30┬░ = 60┬░ Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, x┬░ = 30┬░