தொகுமுறை வகுத்தலைப் பயன்படுத்திக் காரணிப்படுத்துதல் (Factorisation using Synthetic Division)

3. தொகுமுறை வகுத்தலைப் பயன்படுத்திக் காரணிப்படுத்துதல் (Factorisation using Synthetic Division)

ஒரு முப்படிக் கோவையைத் தொகுமுறை வகுத்தலின் உதவியால் எவ்வாறு ஒருபடிக் கோவைகளாகக் காரணிப்படுத்த இயலும் என்பதை இப்பகுதியில் நாம் கற்கலாம். 

கொடுக்கப்பட்ட முப்படிப் பல்லுறுப்புக் கோவை p(x) −க்கு ஒருபடிக் காரணி ஒன்றைத் தெரிந்து கொண்ட பிறகு, தொகுமுறை வகுத்தலைப் பயன்படுத்தி p(x) இன் இருபடிக் காரணியைக் காணலாம். மேலும், அந்த இருபடிக் கோவையை இயலுமெனில் ஒருபடிக் காரணிகளின் பெருக்கற்பலனாகக் காரணிப்படுத்தலாம்.

குறிப்பு: 

• மாறிலிக் கோவை அல்லாத ஒரு பல்லுறுப்புக் கோவை p(x) −க்கு p(a) = 0 என இருந்தால் மட்டுமே x = a என்பது அதன் பூச்சியமாகும். 

• x−a ஆனது p(x) −க்கு ஒரு காரணி என இருந்தால், இருந்தால் மட்டுமே p(a) = 0 ஆகும். (காரணித் தேற்றம்)

ஒரு பல்லுறுப்புக் கோவைக்கு (x − 1) மற்றும் (x + 1) ஆகியன காரணிகளாகுமா என்பதை அடையாளம் காணுதல்: 

• p(x) இன் அனைத்து உறுப்புகளின் கெழுக்கள் மற்றும் மாறிலி உறுப்பின் கூடுதல் பூச்சியம் என இருந்தால், இருந்தால் மட்டுமே p(x) −க்கு (.x−1) ஒரு காரணியாகும். 

• p(x) இன் இரட்டைப் படை அடுக்குகளில் உள்ள உறுப்புகளின் கெழுக்கள் மற்றும் மாறிலி உறுப்புகளின் கூடுதலானது ஒற்றைப்படை அடுக்குகளில் உள்ள உறுப்புகளின் கெழுக்களின் கூடுதலுக்குச் சமம் என இருந்தால், இருந்தால் மட்டுமே (x+1) ஆனது p(x) −க்கு ஒரு காரணியாகும்.

எடுத்துக்காட்டு 3.38

 (i) x3 – 7x2 + 13x − 7 −க்கு (x − 1) ஒரு காரணியாகும் என நிரூபி.

(ii) x3 + 7x2 + 13x + 7 −க்கு (x + 1) ஒரு காரணியாகும் என நிரூபி. 

தீர்வு

(i) p(x) = x3 – 7x2 + 13x − 7 என்க.

கெழுக்களின் கூடுதல் = 1−7+13−7 =0

எனவே, (x − 1) என்பது p(x) இன் ஒரு காரணி. 

(ii) q(x) = x3 + 7x2 + 13x +7 என்க .

இரட்டைப்படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்களின் கூடுதல் =7+7 = 14 

ஒற்றைப்படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்களின் கூடுதல் = 1+ 13 = 14 

எனவே, (x + 1) என்பது q(x) இன் ஒரு காரணி.

எடுத்துக்காட்டு 3.39

 x3 + 13x2 + 32x + 20 ஐ நேரிய காரணிகளாகக் காரணிப்படுத்துக. 

தீர்வு

 p(x) = x3 + 13x2 + 32x + 20 என்க. 

அனைத்து உறுப்புகளின் கெழுக்களின் கூடுதல் = 1+13+ 32 + 20 = 66 ≠ 0

எனவே, (x−1) என்பது ஒரு காரணியல்ல. 

இரட்டைப்படை அடுக்கு கொண்ட உறுப்பின் கெழு மற்றும் மாறிலியின் கூடுதல் = 13 + 20 = 33 

ஒற்றைப்படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்களின் கூடுதல் = 1 + 32 = 33

ஆகவே, (x + 1) என்பது p(x) இன் ஒரு காரணி.

மற்ற நேரிய காரணிகளைக் காணத் தொகுமுறை வகுத்தல் முறையைப் பயன்படுத்துவோம்.

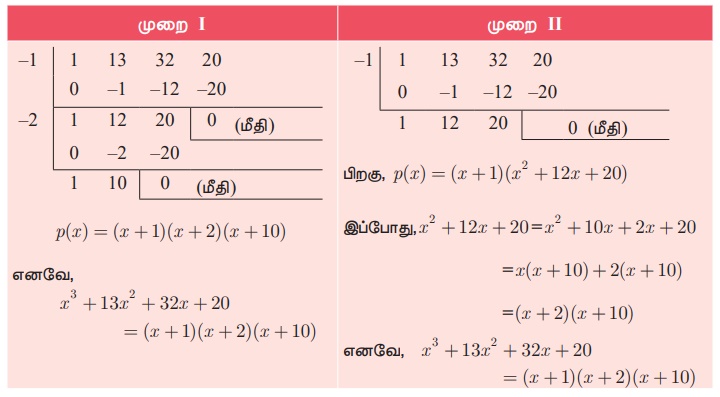
எடுத்துக்காட்டு 3.40

 x3 – 5x2 – 2x + 24 ஐக் காரணிப்படுத்துக.

தீர்வு

 p(x) = x3 – 5x2 – 2x + 24 என்க.

 x = 1 எனில் p(1) = 1−5−2+24 = 18 ≠ 0  (x − 1) ஒரு காரணியல்ல.

 x = –1 எனில் p(−1) = −1−5+2+ 24 = 20 ≠ 0 (x + 1) ஒரு காரணியல்ல.

ஆகவே, மற்ற x இன் காரணிகளைக் காண முயன்று தவறிக் கற்றல் (trial and error method) முறையைப் பயன்படுத்தவும்.

 x = 2 எனில், 

p(2) = 23 – 5(2)2 – 2(2) + 24

= 8 − 20 − 4 +24

= 8 ≠ 0

ஆகவே, (x−2) ஒரு காரணியல்ல

x = −2 எனில்,

 p(−2) = (−2)3 − 5(−2)2 − 2(−2) + 24

= −8 – 20 + 4 + 24

 p(−2) = 0

ஆகவே, (x+2) ஒரு காரணியாகும்

எனவே, (x + 2) (x – 3) (x – 4) ஆகியன காரணிகள்.

ஆகவே, x3 – 5x2 – 2x2 + 24 = (x + 2)(x − 3)(x − 4)

குறிப்பு:  x2 – 7x + 12 −க்கு 3 ஆனது ஒரு பூச்சியமா என சோதிக்கும்போது, 3 ஒரு  பூச்சியமில்லை எனில், −3 அல்லது 4 அல்லது, −4 ... பூச்சியமா எனச் சோதிக்க.