ஐக்கோபியின் முற்றொருமை மற்றும் லாக்ராஞ்சியின் முற்றொருமை (Jacobi's Identity and Lagrange's Identity)

ஐக்கோபியின் முற்றொருமை மற்றும் லாக்ராஞ்சியின் முற்றொருமை (Jacobi's Identity and Lagrange's Identity)

தேற்றம் 6.9 (ஜக்கோபியின் முற்றொருமை) (Jacobi's identity)

என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில், 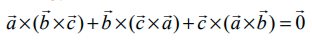ஆகும்.

நிரூபணம்

வெக்டர் முப்பெருக்கலின் விரிவாக்கத்தைப் பயன்படுத்தி பின்வருவனவற்றைப் பெறுகிறோம்.

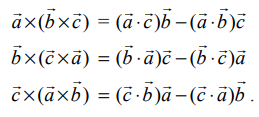
இச்சமன்பாடுகளின் கூடுதலைக் கண்டுபிடித்து இரு வெக்டர்களுக்கான திசையிலிப் பெருக்கலின் பரிமாற்று விதியைப் பயன்படுத்தினால், 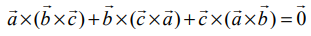  எனப் பெறுகிறோம். 

தேற்றம் 6.10 (லாக்ராஞ்சியின் முற்றொருமை) (Lagrange's identity)

என்பன ஏதேனும் நான்கு வெக்டர்கள் எனில்,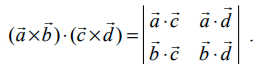

நிரூபணம்

திசையிலி முப்பெருக்கலில் புள்ளி மற்றும் வெக்டர் குறிகளை இடமாற்றம் செய்யலாம் என்பதால், 

எடுத்துக்காட்டு 6.19

என நிறுவுக.

தீர்வு

திசையிலி முப்பெருக்கலின் வரையறையைப் பயன்படுத்தி நாம் பெறுவது

எடுத்துக்காட்டு 6.20

என நிறுவுக.

தீர்வு

கொடுக்கப்பட்ட சமன்பாட்டின் வலதுபுறம் உள்ள வெக்டரில் −ஐ வெக்டர் முப்பெருக்கலின் முதல் வெக்டராக எடுத்துக்கொண்டு –ன் விரிவாக்கம் காண்போம். எனவே,

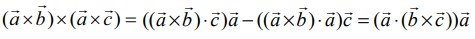
எடுத்துக்காட்டு 6.21

சமன்பாடுகள் (1) மற்றும் (2) ஆகியவற்றிலிருந்து, முற்றொருமை (i) நிறுவப்பட்டது. முற்றொருமை (ii)−ன் சரிபார்த்தல் மாணவர்களின் பயிற்சிக்காக விடப்பட்டுள்ளது.