11 வது கணக்கு : அலகு 8 : வெக்டர் இயற்கணிதம் (Vector Algebra)
வெக்டர் பெருக்கம் (Vector product) மற்றும் பண்புகள்
வெக்டர் பெருக்கம் (Vector product)
இரு வெக்டர்களுக்கு இடையேயான வெக்டர் பெருக்கத்தை வரையறுக்க வலக்கை முறை மற்றும் இடக்கை முறை ஆகியவற்றின் கருத்தாக்கம் தேவைப்படுகிறது.
வலது கையின் விரல்களை 
உடன் ஒன்றுமாறு வைத்து விரல்களை −லிருந்து 
இருக்கும் திசை நோக்கி மடக்கினால் (கோணம் 180°க்கு குறைவாக இருக்க வேண்டும்), நமது கட்டை விரலானது × −ன் திசையை குறிக்கும். இப்போது வலக்கை முறையின்படி × −ன் திசையானது × −க்கு எதிர் திசையில் இருக்கும் (படம் 8.38−ஐ பார்க்க).
மேலும் நாம் −ஐ −ன் திசையை நோக்கி θ கோணம் (<π) திருப்பினால்
× −ன் திசையானது வலக்கை முறையில் அமைந்த திருகு நகரும் திசையிலேயே அமையும் எனக் காணலாம்.
ஒரு கார்டீசியன் ஆயத்தொலை முறை ஒரு வலக்கை முறையை அமைக்க வேண்டுமாயின் அச்சுகளின் மிகைத் திசையில் அலகு வெக்டர்களான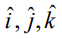 
என்பவை படம் 8.39−ல் உள்ளது போன்று அமைய வேண்டும். 
−ன் திசையானது படம் 8.40−ல் உள்ளவாறு அமைந்தால் அதனை இடக்கை முறை என்கிறோம்.
வரையறை 8.17
× ஆனது || || sin θ என்கிற எண்ணளவையும் 
என்ற திசையையும் கொண்ட ஒரு வெக்டர் ஆகும்.
இது மட்டுமல்லாமல் × ஆனது மற்றும் உள்ள தளத்திற்குச் செங்குத்தாக இருக்கும்.
குறிப்பு 8.6
(i) −ன் திசையைக் கணிப்பதற்கு மற்றும் −ன் வரிசை மிகவும் முக்கியமானதாகும்.
(ii) வெக்டர் பெருக்கலின் போது கிடைப்பது ஒரு வெக்டர். எனவே இதனை வெக்டர் பெருக்கம் என்று அழைக்கிறோம். இந்த பெருக்கத்தை குறிப்பிட ‘×' என்ற குறியீட்டைப் பயன்படுத்துகின்றோம். எனவே இதனை குறுக்குப் பெருக்கம் என்றும் அழைக்கலாம்.
வெக்டர் பெருக்கத்தின் வடிவக் கணித விளக்கம் (Geometrical interpretation of vector product)
ஆகியவை அடுத்தடுத்த பக்கங்களாகக் கொண்டு OACB என்ற இணைகரத்தைப் பூர்த்தி செய்க.
இதிலிருந்து இணைகரம் OACB−ன் பரப்பளவில் பாதியானது, முக்கோணம் OAC−ன் பரப்பு என வருவிக்கலாம்.
வருவித்தல்
மற்றும் ஐ அடுத்தடுத்த பக்கங்களாகக் கொண்ட முக்கோணத்தின் பரப்பு =1/2 ×
பண்புகள்
(i) வெக்டர் பெருக்கம் பரிமாற்ற விதிக்கு உட்படாது. வரையறையிலிருந்து,
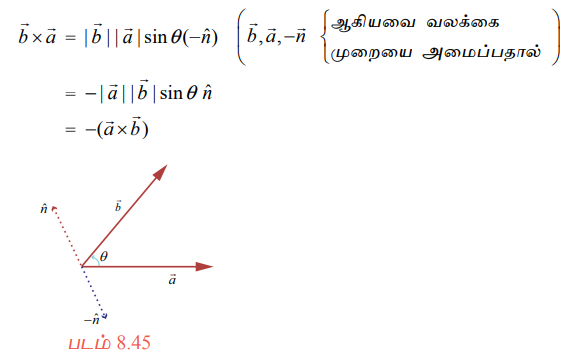
எனவே வெக்டர் பெருக்கம் பரிமாற்றத்தக்கதல்ல.
குறிப்பு 8.7
இதில் θ எப்பொழுதும் குறுங்கோணமாகவே அமையும். எனவே வெக்டர் பெருக்கத்தைப் பயன்படுத்தி இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணத்தைக் காணும்போது எப்பொழுதும் குறுங்கோணம் மட்டுமே நமக்கு கிடைக்கும். ஆகவே கோணங்களைக் கணக்கிடப் புள்ளிப் பெருக்கத்தைப் பயன்படுத்துவதே சிறந்தது. இதன்மூலம் θ அமையும் இடத்தை அறிய முடியும்.
குறிப்பு 8.8
−க்கு பதிலாக எந்த இரண்டு பக்கங்களைக் கொண்டும் தீர்வு காணலாம்.
பாடத் தொகுப்பு
இப்பாடப்பகுதியில் நாம் கற்றுத் தெளிந்தவை
• எண்ணளவைக் கொண்டு தீர்மானிக்கப்படும் கணியம் திசையிலி ஆகும்.
• எண்ணளவு மற்றும் திசை ஆகியவற்றைக் கொண்டு தீர்மானிக்கப்படும் கணியம் வெக்டர் ஆகும்.
• எந்தவொரு புள்ளியையும் ஒரு வெக்டரின் ஆதிப்புள்ளியாகத் தேர்ந்தெடுக்க முடியுமானால் அது கட்டிலா வெக்டர் ஆகும். ஆனால் ஒரு குறிப்பிட்ட புள்ளியை மட்டுமே ஆதிப்புள்ளியாகத் தேர்ந்தெடுக்க முடியுமானால் அது அறுதியிட்ட வெக்டர் ஆகும்.
• ஒரே தளத்தின் மீது அமைந்த அல்லது அந்தத் தளத்திற்கு இணையாக அமைந்த இரண்டு அல்லது அதற்கு மேற்பட்ட வெக்டர்கள் ஒரே தள அமை வெக்டர்கள் ஆகும்.
• இரு வெக்டர்களின் எண்ணளவுகள் சமமாகவும் அவை ஒரே திசையினையும் பெற்றிருந்தால் அவற்றைச் சமவெக்டர்கள் எனலாம்.
• ஒரு வெக்டரின் எண்மதிப்பு 0 எனில் அது பூஜ்ஜிய வெக்டர் ஆகும்.
• ஒரு வெக்டரின் எண்ணளவு 1 எனில் அது அலகு வெக்டர் ஆகும்.
• என்பது ஏதேனும் ஒரு வெக்டர், m ஒரு திசையிலியாயின் m என்பது வெக்டர் உடன் திசையிலி m−ன் திசையிலிப் பெருக்கம் ஆகும்.
• மற்றும் என்ற இரு வெக்டர்கள் இணை எனில், 
. இங்கு λ ஓர் திசையிலி.
• மற்றும் ஆகியவை முக்கோணத்தின் வரிசையாக எடுக்கப்பட்ட பக்கங்கள் எனில், 
• வெக்டர்களின் கூட்டல், சேர்ப்புப் பண்புக்கு உட்படும்.
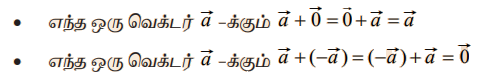
• வெக்டர் கூட்டல் பரிமாற்றுப் பண்புடையது.
• இரு வெக்டர்கள் அவற்றின் எண்ணாலும் திசையாலும் ஒரு முக்கோணத்தின் வரிசையாக எடுக்கப்பட்ட இரண்டு பக்கங்களின் மூலமாக குறிப்பிடப்பட்டால், அவற்றின் கூடுதல் அம்முக்கோணத்தின் எதிர்வரிசையில் எடுக்கப்பட்ட மூன்றாவது பக்கமாகும். இதுவே வெக்டர் கூட்டலின் முக்கோண விதி.
• OABC என்ற இணைகரத்தில் 
ஆகியவை அடுத்தடுத்த பக்கங்களாயின், அதன் மூலைவிட்டம் 
இவற்றின் கூடுதலைக் குறிக்கும். இதுவே வெக்டர் கூட்டலின் இணை6கர விதியாகும்.
• α , β , γ ஆகியவை திசைக் கோணங்கள் எனில், cos α, cos β, cos γ ஆகியவை திசைக்கொசைன்களாகும்.
• 
என்ற வெக்டரின் திசை விகிதங்கள் x, y, z ஆகும்.
(iv) l, m, n ஆகியவை ஒரு வெக்டரின் திசைக் கொசைன்கள் எனில், l2 + m2 + n2 = 1.
இணையச் செயல்பாடு 8 (a)
வெக்டர் இயற்கணிதம்
படி − 1
கீழ்க்காணும் உரலி / விரைவுக் குறியீட்டைப் பயன்படுத்தி GeoGebra−வின் "XI standard Vector Algebra" பக்கத்திற்குச் செல்க. உங்கள் பாடம் சார்ந்த பல பணித்தாள்கள் இப்பக்கத்தில் கொடுக்கப்பட்டிருக்கும்.
படி −2
"Direction Cosines பயிற்சித்தாளைத் தேர்வு செய்து நழுவல்களை நகர்த்தியதும் 3−D உருவமைப்பு வலப்பக்கம் காணப்படும். 3−D உருவமைப்பைச்சுழற்ற சுட்டியை வலப்பக்கம் சொடுக்கி பல்வேறு அமைப்புகளைக் காணலாம். நழுவல்களை நகர்த்தி, அல்லது x, y மற்றும்: மதிப்புகளைப் பதிந்து திசையெண்ணை மாற்றலாம்
உரலி :
https://ggbm.at/cem3sdq5
*படங்கள் அடையாளத்திற்கு மட்டும்.
இணையச் செயல்பாடு 8 (b)
வெக்டர் இயற்கணிதம்
படி − 1
கீழ்க்காணும் உரலி / விரைவுக் குறியீட்டைப் பயன்படுத்தி GeoGebra−வின் "XI standard Vector Algebra" பக்கத்திற்குச் செல்க. உங்கள் பாடம் சார்ந்த பல பயிற்சித்தாள்கள் இப்பக்கத்தில் கொடுக்கப்பட்டிருக்கும்.
படி − 2
"Product of Vectors" பயிற்சித்தாளைத் தேர்வு செய்து நழுவல்களை நகர்த்தியதும் 3−D உருவமைப்பு வலப்பக்கம் காணப்படும். 3−D உருவமைப்பைச் சுழற்ற சுட்டியை வலப்பக்கம் சொடுக்கி பல்வேறு அமைப்புகளைக் காணலாம். நழுவல்களை நகர்த்தி, அல்லது x, y மற்றும் z மதிப்புகளைப் பதிந்து திசையெண்ணை மாற்றலாம் (நன்றாகப் புரிந்து கொள்ள a1, a2, மற்றும் a3 மதிப்புகளை மாற்ற வேண்டாம்) AB×AC அவற்றின் கூறுகள் நேர்குத்தாகக் கொடுக்கபட்டுள்ளது.
உரலி :
*படங்கள் அடையாளத்திற்கு மட்டும்.