மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு

மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு (Mean or Average value of AC)

ஒரு நேர்திசை மின்னோட்ட அமைப்பில் மின்னோட்டம் மற்றும் மின்னழுத்த வேறுபாடு நேரத்தைப் பொருத்து மாறாமல் உள்ளன. எனவே அவற்றின் எண்மதிப்புகளைக் குறிப்பிடுவதில் சிரமம் ஏதுமில்லை. ஆனால் ஒரு மாறுதிசை மின்னோட்டம் அல்லது மின்னழுத்த வேறுபாடு நேரத்திற்கு நேரம் மாறுபடுகிறது. ஆகவே, ஒரு மாறுதிசை மின்னோட்டம் அல்லது மின்னழுத்த வேறுபாட்டின் எண்மதிப்பை எவ்வாறு குறிப்பிடுவது என்ற கேள்வி எழுகிறது. அதனைக் குறிப்பிட பல வழிகள் இருந்தாலும், மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு மற்றும் RMS (Root Mean Square) மதிப்பு ஆகிய இரு வழிகளை மட்டும் நமது விவாதத்திற்கு எடுத்துக்கொள்வோம்.

மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு

ஒரு சுற்றில் மாறுதிசை மின்னோட்டத்தின் எண் மதிப்பு நேரத்திற்கு நேரம் மாறிக் கொண்டே இருக்கிறது மற்றும் அதன் திசையானது ஒவ்வொரு அரை சுற்றிற்கும் எதிர்த்திசையில் திருப்பப்படுகிறது என அறிந்துள்ளோம். நேர் அரை சுற்றின் போது மின்னோட்டம் நேர்க்குறியாக கொள்ளப்படுகிறது மற்றும் எதிர் அரைசுற்றில் அது எதிர்க்குறியாகும். எனவே ஒரு முழு சுற்றிற்கான சமச்சீர் மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு சுழி ஆகும்.

எனவே, சராசரி மதிப்பானது ஒரு சுற்றின் பாதிக்கு மட்டும் அளவிடப்படுகிறது. சராசரி மின்னோட்டம் மற்றும் சராசரிமின்னழுத்த வேறுபாடு ஆகிய மின் சொற்கள், மாறுதிசை மற்றும் நேர்திசை மின்னோட்ட சுற்றுகளை பகுப்பாய்வு செய்வதிலும், கணக்கீடுகளிலும் பயன்படுத்தப்படுகின்றன.

மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு என்பது ஒரு நேர் அரைச்சுற்று அல்லது எதிர் அரைச்சுற்றில் உள்ள மின்னோட்டத்தின் அனைத்து மதிப்புகளின் சராசரி என வரையறுக்கப்படுகிறது.

சைன் வடிவ மாறுதிசை மின்னோட்டத்தின் கணநேர மதிப்பு i = I_m sin wt = I_m sinθ (இங்குθ = wt) என்ற சமன்பாட்டால் குறிப்பிடப்படுகிறது. அதன் வரைபடம் படம் 4.36- இல் காட்டப்பட்டுள்ளது.

ஒரு அரைச்சுற்றில் உள்ள அனைத்து மின்னோட்டங்களின் கூடுதல், நேர் அரைச்சுற்றின் (அல்லது எதிர் அரைச்சுற்று) பரப்பிற்குச் சமமாகும். எனவே,

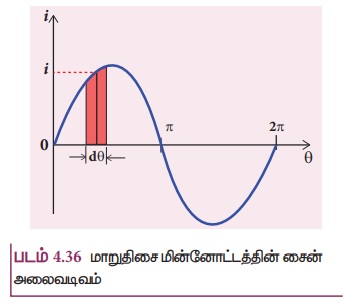
மின்னோட்ட அலையின் நேர் அரைச்சுற்றில் dθ தடிமன் கொண்ட ஒரு சிறு பட்டையைக் கருதுக (படம் 4.36). i என்பது அந்த பட்டையின் மையப்புள்ளிக்கான மின்னோட்ட மதிப்பு எனக்கொள்க.

சிறு பட்டையின் பரப்பு = i dθ

நேர் அரைச்சுற்றின் பரப்பு

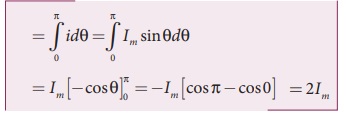
அரைச்சுற்றின் அடிப்பக்க நீளம் πஆகும். இதனை சமன்பாடு (4.31) இல் பிரதியிட, நாம் பெறுவது மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பு

எனவே மாறுதிசை மின்னோட்டத்தின் சராசரி மதிப்பானது, அதன் பெரும மதிப்பின் 0.637 மடங்கு ஆகும். எதிர் அரைச்சுற்றுக்கு, I_av = -0.637 I_m.

குறிப்பு

உதாரணமாக மாறுதிசை மின்னோட்டத்தின் ஒரு அரைச்சுற்றில் i₁, i₂, ...i_n என n மின்னோட்டங்களை நாம் கருதினால், அதன் சராசரி மதிப்பு வருமாறு

I_av=அரைச்சுற்றில் உள்ள அனைத்துமின்னோட்டங்களின் கூடுதல்/ மின்னோட்டங்களின் எண்ணிக்கை Iav= i1+i2 +....+in/n