எல்லைகள் (Limits)

எல்லைகள் (Limits)

1. எல்லைகளைக் காணுதல் (The calculation of limits)

நவீனக் கணிதத்திலும், நுண்கணிதத்திலும் முக்கிய பங்காற்றும் எல்லை பற்றிய கருத்துகளை இந்த அத்தியாயத்தில் விரிவாக காண்போம். கணிதவியல் 3000 ஆண்டுகளுக்கு முற்பட்டது என்றாலும், 19−ம் நூற்றாண்டில் பிரெஞ்சுக் கணித மேதை அகஸ்டின் −லூயிஸ் கோஷி மற்றும் கார்ல் வொயர்ஸ்ட்ராஸ் ஆகியோர் குறிப்பிடும் வரை எல்லை பற்றி அறிந்திருக்கவில்லை. இப்பகுதியில் எல்லையின் வரையறை மற்றும் அவற்றை எவ்வாறு காண்பது என்பதைப் பற்றியும் பார்ப்போம். 

விளக்க எடுத்துக்காட்டு 9.1

f : ℝ → ℝ என்ற சார்பு y = f (x ) = x2 + 3 என வரையறுப்பதாக எடுத்துக் கொள்வோம். 

x = 2 என்ற புள்ளியில் இந்தச் சார்பின் தன்மை பற்றி ஆராய்வோம். இருவிதமான x−ன் மதிப்புகளைப் பயன்படுத்துவோம் : ஒன்று 2−ன் இடப்பக்கமிருந்து (2−க்கு குறைவானது) 2−ஐ நோக்கி நெருங்கும் மதிப்புகள் ; மற்றொன்று 2−ன் வலப்பக்கமிருந்து 2−ஐ நோக்கி நெருங்கும் மதிப்புகள் (2க்கு அதிகமான).

அட்டவணையிலிருந்து x−ன் மதிப்பு 2−ஐ நோக்கி நெருங்கும்போது f(x) = x2 + 3−ன் மதிப்பு 7−ஐ நெருங்குவதைக் காணலாம். இதில் வியக்கத்தக்கது ஒன்றுமில்லை, ஏனெனில் x = 2−ல் f(x)−ன் மதிப்பை கணக்கிடும்போது f(2) = 22 + 3 = 7 எனக்கிடைப்பதைக் காணலாம்.

இந்த எல்லை மதிப்பை யூகிப்பதற்கு x = 2−ல் f(x)−ன்மதிப்பைக் கணக்கிட வேண்டிய அவசியமில்லை. 

x−ன் மதிப்பு 2−க்கு இடமிருந்தும் (2−ஐ விட குறைவான மதிப்புகள்) வலமிருந்தும் (2−ஐ விட அதிக மதிப்புகள்) 2−ஐ நெருங்கும்போது f(x)−ன் மதிப்பு 7−ஐ நெருங்குகிறது. அதாவது x−ன் மதிப்பு 2−க்கு மிக நெருக்கமாக அமையும்போது f(x)−ன் மதிப்பு 7−க்கு மிக அருகில் அமைகிறது. இந்தச் சூழலை சுருக்கமாக பின்வருமாறு கூறலாம்.

x−ன் மதிப்பு 2−ஐ இடப்பக்கமாக நெருங்கும்போது f(x)−ன் இடது எல்லை 7−ஆகவும், அதேபோல் x−ன் மதிப்பு 2−ஐ வலப்பக்கமாக நெருங்கும்போது f(x)−ன் வலது எல்லை 7−ஆகவும் உள்ளது என்று பொருள். இதனைப் பின்வருமாறு எழுதலாம் :

என்பது தனித்த ஒரு மெய்யெண் என்பதையும் குறிக்கும்.

x → 2 எனும்போது f(x) = x2 + 3−ன் தன்மையை, படம் 9.1 வடிவியல் முறையில் விளக்குகிறது.

விளக்க எடுத்துக்காட்டு 9.2

அடுத்ததாக f(x) = 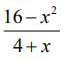 என்ற விகிதமுறு சார்பை எடுத்துக்கொள்வோம்.

இந்தச் சார்பின் மதிப்பகம் ℝ \ {− 4} ஆகும். f(−4) வரையறுக்கப்படவில்லை. எனினும், x −ன்  மதிப்பு − 4ஐ நெருங்கும்போது உள்ள f(x)−ன் மதிப்பைக் கணக்கிட இயலும், ஏனெனில், என்ற குறியீட்டின்படி நாம் x−க்கு – 4 அருகில் உள்ள மதிப்புகளை மட்டுமே கருத்தில் கொள்கிறோம். x = −4 அல்ல என்பதை இது குறிக்கின்றது. பின்வரும் அட்டவணை x−ன் மதிப்பு − 4ஐ நெருங்கும்போது உள்ள f(x)−ன் மதிப்புகளைத் தருகிறது,

x ≠ − 4 எனில், f(x)−ஐ நீக்கல் முறையில் சுருக்கலாம் :

f(x) = (16 − x2) /(4+x) = (4 + x)(4 − x) / (4 + x) = 4  − x.

படம் 9.2 லிருந்து, f(x)−ன் வரைபடமானது x = −4 என்ற புள்ளியைத் தவிர மற்ற இடங்களில் y = 4 − x என்ற கோட்டின் வரைபடம் அமைந்துள்ளதைக் காணலாம். x = −4 என்ற புள்ளி சிறு துவாரமாகத் (puncture) தொடர்ச்சியற்றுக் காட்டப்பட்டுள்ளது. x−ன் மதிப்பு −4−ஐ நெருங்க, நெருங்க y−ன் மதிப்பு 8−ஐ நெருங்கி, நெருங்கி செல்வதைக் காணலாம். இவை படத்தில் x−அச்சின் மீதுள்ள அம்புக்குறிகளையும், y−அச்சின் மீதுள்ள அம்புக்குறிகளையும் குறிக்கின்றன.

இங்கு

விளக்க எடுத்துக்காட்டு 9.2−ல் x = −4இல் f(x) வரையறுக்கப்படவில்லை எனினும் x−ன் மதிப்பு − 4ஐ நெருங்கும்போது f(x)−ன் மதிப்பு ஒரு எல்லையை நெருங்குவதைக் காணலாம். x = −4−ல் சார்பு f(x)−ன் மதிப்பு இருந்தாலும், இல்லாமல் இருந்தாலும் அது x−ன் மதிப்பு −4 −ஐ நெருங்கும்போது f(x)−ன் எல்லை மதிப்பு இருத்தலைப் பாதிக்கவில்லை என்பதை உணரலாம்.

விளக்க எடுத்துக்காட்டு 9.3

தற்போது நாம் விளக்க எடுத்துக்காட்டுகள் 9.1 மற்றும் 9.2−லிருந்து வேறுபட்ட ஒரு சார்பை எடுத்துக் கொள்வோம்.

x = 0 என்ற மதிப்பு f(x) என்ற சார்பின் சார்பகமான ℝ \{0}−ல் இல்லை. வரைபடத்தைக் கவனிக்கவும். வரைபடத்தில் இருந்து x−ன் மிகை மதிப்புகளுக்கு,

எனவும் உள்ளதைக் காணலாம்.

x−ன் மதிப்பு பூஜ்ஜியத்திற்கு எவ்வளவு மிக அருகில் இருந்தாலும் (பூஜ்ஜியத்தின் அண்மையில்), x−ன் மிகை மற்றும் குறை மதிப்புகளுக்கு முறையே  f(x) = 1 மற்றும்  f(x) = − 1 எனுமாறு இருக்கும் என அறியலாம்.

இதிலிருந்து x = 0 −ல் எல்லை மதிப்பு இல்லை என அறியலாம். ஆனால்,x−ன் மற்ற மதிப்புகளுக்கு எல்லை மதிப்புகள் உண்டு.

அதாவது x0 ≠ 0 என உள்ள எல்லா மெய்யெண்களுக்கும்,

இப்போது 9.1 முதல் 9.3 வரையிலான விளக்க எடுத்துக்காட்டுகளின் வேறுபாடுகளைக் காண்போம். விளக்க எடுத்துக்காட்டு 9.1−ல் f(x) = x2 + 3 என்ற சார்பு x = 2−ல் வரையறுக்கப்பட்டுள்ளது. அதாவது 2 என்ற எண் ℝ = (– ∞, ∞) என்ற சார்பகத்தில் உள்ளது. விளக்க எடுத்துக்காட்டு 9.2−ல்  x = −4 என்ற புள்ளியில் சார்பு வரையறுக்கப்படவில்லை. 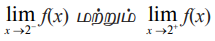முதலில் கூறப்பட்ட எடுத்துக்காட்டில் x−ன் மதிப்பு 2−ஐ நெருங்க நெருங்க கிடைக்கக் கூடியதாக அதாவது கிடைக்கப்பெற்று அவை சமமாகவும் ஒரு தனித்த மெய்யெண்ணாகவும் உள்ளன.

இரண்டாவது எடுத்துக்காட்டில் x = −4−ல் சார்பு வரையறுக்கப்படாவிடினும் x−ன் மதிப்பு − 4−ஐ நெருங்க நெருங்க கிடைக்கிறது.

விளக்க எடுத்துக்காட்டு 9.3−ல் −ன் மதிப்பு கிடைக்கப்பெறவில்லை என்பதன் பொருள், x−ன் மதிப்பு பூஜ்ஜியத்திற்கு மிக அருகில் உள்ளபோது ஒரு பக்க எல்லைகளான மற்றும் −ன் மதிப்புகள் வெவ்வாறாக உள்ளன என்பதாகும்.

மேற்கண்ட உற்று நோக்கல்களிலிருந்து எல்லைக்கான வரையறையை உய்த்தறியும் முறையில் பெறலாம்.

வரையறை 9.1

I என்பது x0 ∈ ℝ என்ற புள்ளியை உள்ளடக்கிய ஒரு திறந்த இடைவெளி என்க. சார்பு f : 1 → ℝ. என வரையறுக்கப்பட்டுள்ளது. x−ன் மதிப்பு x0 −ஐ நெருங்கும்போது f(x)−ன் எல்லை மதிப்பு L (அதாவது குறியீட்டில் 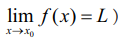எனக் கூற வேண்டுமானால், x ≠ x0 ஆக அமைந்து x−ஆனது தேவையான அளவுக்கு x0 −ஐ இருபுறமுமாக நெருங்கும்போது f(x)−ன் மதிப்பானது தேவையான அளவுக்கு L−க்கு மிக அருகில் அமைய வேண்டும்.

மேற்கூறிய விவரங்களை பின்வரும் வரைபடங்கள் (9.4 மற்றும் 9.5) மூலம் காணலாம்.

2. ஒருபுற எல்லைகள் (One sided limits)

வரையறை 9.2

x−ன் மதிப்பு தேவையான அளவு x0 −க்கு அருகிலும் x0 −ஐ விடக் குறைவாகவும் இருக்கும்போது f(x)−ன் மதிப்பு l1, க்கு மிக அருகில் இருக்கும் எனில், x−ன் மதிப்பு x0 −ஐ நெருங்கும்போது f(x)−ன் இடப்பக்க எல்லை (x இடப்பக்கமிருந்து x0 −ஐ நெருங்கும்போது f(x)−ன் எல்லை) எனக் கூறலாம்.

இதேபோன்று

வரையறை 9.3

x−ன் மதிப்பு தேவையான அளவு x0 −க்கு அருகிலும் x0 −ஐ விட அதிகமாகவும் இருக்கும்போது f(x)−ன் மதிப்பு l2−க்கு மிக அருகில் இருக்கும் எனில், x−ன் மதிப்பு x0 −ஐ நெருங்கும்போது f(x)−ன் வலப்பக்க எல்லை (x வலப்பக்கமிருந்து x0 −ஐ நெருங்கும்போது f(x)−ன் எல்லை) எனக்கூறலாம். 

மேலும் x < x0 மற்றும் x > x0 என்பவை முறையே “x → x0− ” மற்றும் எனக் “x → x0+ ”  குறிக்கப்படுகிறது.

இந்த வரையறைகள் 9.6 முதல் 9.9 வரையிலான படங்கள் மூலம் விளக்கப்பட்டுள்ளன.

x−ன் மதிப்பு x0 −ஐ நெருங்கும்போது f(x)−ன் எல்லை மற்றும் ஒருபுற எல்லைகளின் வரையறைகளிலிருந்து பின்வருவனவற்றை பெறலாம்.

இவ்வாறாக, கிடைக்கப்பெறும் எனில் L ஒரு தனித்த மெய்யெண்ணாகும். மேற்கண்ட நிபந்தனைகளில் ஏதேனும் ஒன்றை நிறைவு செய்யவில்லை எனில் x−ன் மதிப்பு x0−ஐ நெருங்கும்போது f(x)−க்கு எல்லை மதிப்பு இல்லை எனலாம்.

ஒருபுற எல்லைகள், எல்லைகளைவிட வலுக்குறைந்தவையாகும் என்பதனைக் கவனத்தில் கொள்ளவும். ஒருபுற எல்லைகளைக் காண கீழ்க்காண்பவை பயனுள்ளதாக இருக்கும்.

h > 0 எனில்,

குறிப்பாக f(x0−) மற்றும் f(x0+) ஆகியவை முறையே இடப்புற மற்றும் வலப்புற எல்லைகளைக் குறிக்கும்போது f(x0) என்பது x = x0 என்ற புள்ளியில் சார்பின் மதிப்பாகும்.

எடுத்துக்காட்டு 9.1