வரையறை - அணிகளின் வகைகள் (Types of matrices) | 11th Mathematics : UNIT 7 : Matrices and Determinants
11 வது கணக்கு : அலகு 7 : அணிகளும் அணிக்கோவைகளும் (Matrices and Determinants)
அணிகளின் வகைகள் (Types of matrices)
அணிகளின் வகைகள் (Types of matrices)
நிரை, நிரல், பூஜ்ஜிய அணிகள் (Row, Column, Zero matrices)
வரையறை 7.2
ஒரே ஒரு நிரையை மட்டுமே உடைய அணி நிரை அணி எனப்படும்.
எடுத்துக்காட்டாக,
A = [A]1×4 = [1 0 − 1.1 √2] என்பது 1× n வரிசை உடைய நிரை அணியாகும்.
A = [aij]1×n = [aij]1×n என்பது 1×n வரிசை உடைய நிரை அணியின் பொது அமைப்பாகும்.
வரையறை 7.3
ஒரே ஒரு நிரலை மட்டுமே உடைய அணி நிரல் அணி எனப்படும்.
எடுத்துக்காட்டாக, [A]4×1 =  என்பது m×1 வரிசை உடைய நிரல் அணியாகும். இதன் உறுப்புகள் மெய்யெண் சார்புகள் ஆகும். A = [aij]m×1 = [ai1]m×1 என்பது m×1 வரிசை உடைய நிரல் அணியின் பொது வடிவமாகும்.
என்பது m×1 வரிசை உடைய நிரல் அணியாகும். இதன் உறுப்புகள் மெய்யெண் சார்புகள் ஆகும். A = [aij]m×1 = [ai1]m×1 என்பது m×1 வரிசை உடைய நிரல் அணியின் பொது வடிவமாகும்.
வரையறை 7.4
ஓர் அணி A = [aij]m×n −இல் அனைத்து 1 ≤ i ≤ m மற்றும் 1 ≤ j ≤ n மதிப்புகளுக்கும் aij = 0 எனில், இவ்வணி பூஜ்ஜிய அணி எனப்படும். இது O எனக்குறிக்கப்படும்.
எடுத்துக்காட்டாக, [0],  என்பன முறையே 1×1, 3×3, மற்றும் 2 × 4 வரிசை உடைய பூஜ்ஜிய அணிகளாகும்.
என்பன முறையே 1×1, 3×3, மற்றும் 2 × 4 வரிசை உடைய பூஜ்ஜிய அணிகளாகும்.
ஓர் அணி A−ல் குறைந்தபட்சம் ஓர் உறுப்பு பூஜ்ஜியமற்றது எனில், அவ்வணி பூஜ்ஜியமற்ற அணி எனப்படும்.
சதுர, மூலைவிட்ட, அலகு மற்றும் முக்கோண வடிவ அணிகள் (Square, Diagonal, Unit, Triangular matrices)
வரையறை 7.5
ஓர் அணியின் நிரை மற்றும் நிரல்களின் எண்ணிக்கை சமம் எனில், அவ்வணி சதுர அணி எனப்படும். அதாவது, n × n வரிசை உடைய ஒரு சதுர அணி n வரிசை உடைய சதுர அணி எனப்படும்.
எடுத்துக்காட்டாக,  என்பது 3 வரிசையுடைய ஒரு சதுர அணியாகும்.
என்பது 3 வரிசையுடைய ஒரு சதுர அணியாகும்.
வரையறை 7.6
n வரிசை உடைய ஒரு சதுர அணி A= [aij]m×n −ன் உறுப்புகள் a11, a22, a33,… ,amn என்பன முதன்மை மூலைவிட்ட அல்லது பிரதான மூலைவிட்ட உறுப்புகள் எனப்படும்.
வரையறை 7.7
A = [aij]m×n என்ற சதுர அணியில் அனைத்து aij = 0, i # j எனில், அவ்வணி ஒரு மூலைவிட்ட அணி எனப்படும்.
எனவே, ஒரு மூலைவிட்ட அணியில் பிரதான மூலைவிட்ட உறுப்புகளைத் தவிர மற்ற அனைத்து உறுப்புகளும் பூஜ்ஜியமாகும். எடுத்துக்காட்டாக,

என்பன முறையே 3, 2, 1 மற்றும் n வரிசை உடைய மூலைவிட்ட அணிகளாகும். ஒரு பூஜ்ஜிய சதுர அணி ஒரு மூலைவிட்ட அணியாகுமா?
வரையறை 7.8
ஒரு மூலைவிட்ட அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் சமம் எனில், அவ்வணி ஒரு திசையிலி அணி எனப்படும்.
A = [aij]m×n என்ற சதுர அணியில் aij =  எனில்,
எனில்,
A என்ற அணி திசையிலி அணியாகும். இங்கு c என்பது ஒரு நிலை எண்ணாகும்.
எடுத்துக்காட்டாக,

என்பன முறையே வரிசை 3, 2, 1 மற்றும் n உடைய திசையிலி அணிகளாகும்.
மேலும், ஒரு பூஜ்ஜிய சதுர அணி, திசையிலி 0 உடைய திசையிலி அணியாகும் என்பதை கவனத்தில் கொள்க.
வரையறை 7.9
ஒரு சதுர அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் 1 ஆகவும் மற்ற உறுப்புகள் அனைத்தும் பூஜ்ஜியமாகவும் இருந்தால், அவ்வணி அலகு அணி அல்லது சமனி அணி எனப்படும். எனவே,
A = [aij]m×n என்ற சதுர அணியில்  எனில், A என்பது ஓர் அலகு அணியாகும்.
எனில், A என்பது ஓர் அலகு அணியாகும்.
மேலும், n வரிசை உடைய அலகு அணியை In எனக் குறிக்கிறோம்.

என்பன முறையே வரிசை 1, 2, 3 மற்றும் n உடைய அலகு அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
குறிப்பு 7.1
அலகு அணியானது ஒரு திசையிலி அணிக்கு எடுத்துக்காட்டாகும்.
முக்கோண வடிவ அணிகளில், மேல் முக்கோண வடிவ அணி மற்றும் கீழ் முக்கோண வடிவ அணி என இரண்டு வகைகள் உள்ளன.
வரையறை 7.10
ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்குக் கீழ் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில் அவ்வணி மேல் முக்கோண வடிவ அணி எனப்படும்.
எனவே A = [aij]m×n என்ற சதுர அணியில் aij = 0, i > j எனில், அவ்வணி மேல் முக்கோண வடிவ அணியாகும்.
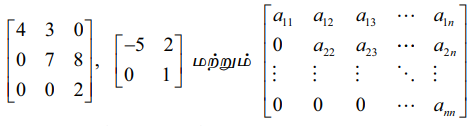 என்பன மேல் முக்கோண வடிவ அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
என்பன மேல் முக்கோண வடிவ அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
வரையறை 7.11
ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்கு மேல் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில், அவ்வணி கீழ் முக்கோண வடிவ அணி எனப்படும்.
எனவே, A = [aij]m×n என்ற சதுர அணியில் aij = 0, i < j எனில், அவ்வணி கீழ் முக்கோண வடிவ அணியாகும்.
 என்பன கீழ் முக்கோண வடிவ அணிகளுக்கு எடுத்துக்காட்டுகளாகும்.
என்பன கீழ் முக்கோண வடிவ அணிகளுக்கு எடுத்துக்காட்டுகளாகும்.
வரையறை 7.12
மேல் முக்கோண வடிவில் அல்லது கீழ் முக்கோண வடிவில் உள்ள ஒரு சதுர அணியை முக்கோண வடிவ அணி என்கிறோம்.
மேலும், ஒரே நேரத்தில் மேல் மற்றும் கீழ் முக்கோண வடிவில் உள்ள ஒரு சதுர அணியானது ஒரு மூலைவிட்ட அணியாக அமைவதைக் காணலாம்.